Template:Crowley2002

D. Crowley, The classification of highly connected manifolds in dimensions 7 and 15, PhD Thesis, Indiana University, Bloomington, 2002. Available at the arXiv:0203253.

Corrections

Remark 1.1. The proof of Lemma 2.16 contains a gap in general. There is a surjection 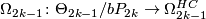$\Omega_{2k-1} \colon \Theta_{2k-1}/bP_{2k} \to \Omega_{2k-1}^{HC}$$\newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\bZ}{\mathbb{Z}} \newcommand{\bR}{\mathbb{R}} \newcommand{\bC}{\mathbb{C}} \newcommand{\bH}{\mathbb{H}} \newcommand{\bQ}{\mathbb{Q}} \newcommand{\bF}{\mathbb{F}} \newcommand{\bN}{\mathbb{N}} \DeclareMathOperator\id{id} % identity map \DeclareMathOperator\Sq{Sq} % Steenrod squares \DeclareMathOperator\Homeo{Homeo} % group of homeomorphisms of a topoloical space \DeclareMathOperator\Diff{Diff} % group of diffeomorphisms of a smooth manifold \DeclareMathOperator\SDiff{SDiff} % diffeomorphism under some constraint \DeclareMathOperator\Hom{Hom} % homomrphism group \DeclareMathOperator\End{End} % endomorphism group \DeclareMathOperator\Aut{Aut} % automorphism group \DeclareMathOperator\Inn{Inn} % inner automorphisms \DeclareMathOperator\Out{Out} % outer automorphism group \DeclareMathOperator\vol{vol} % volume \newcommand{\GL}{\text{GL}} % general linear group \newcommand{\SL}{\text{SL}} % special linear group \newcommand{\SO}{\text{SO}} % special orthogonal group \newcommand{\O}{\text{O}} % orthogonal group \newcommand{\SU}{\text{SU}} % special unitary group \newcommand{\Spin}{\text{Spin}} % Spin group \newcommand{\RP}{\Rr\mathrm P} % real projective space \newcommand{\CP}{\Cc\mathrm P} % complex projective space \newcommand{\HP}{\Hh\mathrm P} % quaternionic projective space \newcommand{\Top}{\mathrm{Top}} % topological category \newcommand{\PL}{\mathrm{PL}} % piecewise linear category \newcommand{\Cat}{\mathrm{Cat}} % any category \newcommand{\KS}{\text{KS}} % Kirby-Siebenmann class \newcommand{\Hud}{\text{Hud}} % Hudson torus \newcommand{\Ker}{\text{Ker}} % Kernel \newcommand{\underbar}{\underline} %Classifying Spaces for Families of Subgroups \newcommand{\textup}{\text} \newcommand{\sp}{^}\Omega_{2k-1} \colon \Theta_{2k-1}/bP_{2k} \to \Omega_{2k-1}^{HC}$ but at the time of writing it is in general open whether 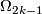$\Omega_{2k-1}$$\Omega_{2k-1}$ is injective.

However, 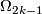$\Omega_{2k-1}$$\Omega_{2k-1}$ is injective for 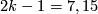$2k-1 = 7, 15$$2k-1 = 7, 15$ by [Wall1962a, Theorem 4] and these are the dimensions in which Lemma 2.16 is used in other parts of the Thesis. For more information about 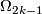$\Omega_{2k-1}$$\Omega_{2k-1}$ see [Stolz1985, Introduction, Theorem B].

Remark 1.2. The expressions for 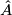$\hat A$$\hat A$ on p.51 are wrong. A factor of 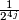$\frac{1}{2^{4j}}$$\frac{1}{2^{4j}}$ needs to be added before each 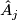$\hat A_j$$\hat A_j$; e.g. $A_1 = \frac{-1}{24}p_1$$A_1 = \frac{-1}{24}p_1$.

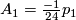Remark 1.3. Definition 2.22 of the linking form is not conventional and Remark 2.23 that all three definitions of the linking form agree is incorrect. In fact, the presentation defintion of the linking form differs from the usual definition of the linking form by a sign. Hence, it would fit better with conventions to define

$\displaystyle b(P) : = -b(\lambda) .$ $$\displaystyle b(P) : = -b(\lambda) .$$

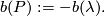
For the explanation of this sign see [Alexander&Hamrick&Vick1976, The proof of Theorem 2.1] and [Gordon&Litherland1978, Section 3].

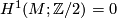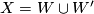Remark 1.4.Theorem 2.55 is not correct as stated: $M$$M$ must be a closed spin $(4k-1)$$(4k-1)$-dimensional rational homology sphere with the extra hypothesis that $H^1(M; \Zz/2) = 0$$H^1(M; \Zz/2) = 0$. This last hypothesis is needed to ensure that $M$$M$ has a unique spin structure and hence that the manifold $X = W \cup W'$$X = W \cup W'$ appearing in the proof admits a spin structure.