Talk:Supplement I (Ex)
Before stating the exercise, we recall the definition of 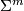 , and explain why it is indeed a simplicial complex.
, and explain why it is indeed a simplicial complex.
Definition 0.1.
The simplicial complex 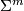 is defined to have
is defined to have  -simplices equal to the set of
-simplices equal to the set of 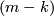 -simplices of
-simplices of 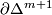 , denoted by
, denoted by 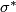 for
for 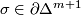 . The face relations are given by
. The face relations are given by 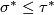 iff
iff 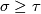 .
.
Lemma 0.2. This is a simplicial complex.
Proof.
The following is an equivalent definition of 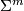 :
:
- Its vertices are the
 -dimensional faces in
-dimensional faces in 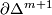 .
.
- A collection of vertices of
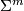 -- i.e.
-- i.e.  -dimensional faces in
-dimensional faces in 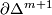 -- is a simplex of
-- is a simplex of 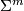 iff the intersecion of all the faces is non-trivial.
iff the intersecion of all the faces is non-trivial.
This is an equivalent definition because of the following special ('miraculous'!) property of 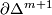 :
:
- The
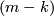 -simplices are precisely the
-simplices are precisely the  -fold intersections of
-fold intersections of  -simplices.
-simplices.
This equivalent description makes it clear that 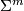 is a simplicial complex, since a subcollection of a non-trivially intersecting collection is again non-trivially intersecting.
is a simplicial complex, since a subcollection of a non-trivially intersecting collection is again non-trivially intersecting.

Remark 0.3.
The first description of 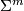 gives us a 'map' of simplicial complexes
gives us a 'map' of simplicial complexes
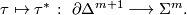
This is of course not a real map of simplicial complexes, since it sends  -simplices to
-simplices to 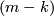 -simplices. However, it does induce a map of barycentric subdivisions
-simplices. However, it does induce a map of barycentric subdivisions
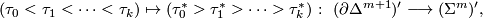
which is an isomorphism of simplicial complexes. So we may view subcomplexes of 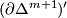 as living in
as living in 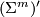 via this isomorphism.
via this isomorphism.
Exercise 0.4.
Let  be a subcomplex of
be a subcomplex of 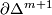 , and consider the barycentric subdivision
, and consider the barycentric subdivision 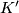 as a subcomplex of
as a subcomplex of 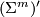 . Show that
. Show that
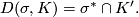
Solution 0.5.
First consider what happens if we view everything as living inside 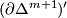 :
:
- The barycentric subdivision
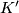 is the subcomplex with
is the subcomplex with  -simplices
-simplices 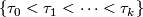 with
with 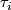 a simplex of
a simplex of  for each
for each  .
.
- The dual complex
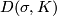 is by definition the subcomplex of
is by definition the subcomplex of 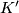 whose
whose  -simplices are
-simplices are 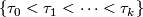 with
with 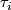 a simplex of
a simplex of  and
and 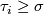 for each
for each  .
.
- Finally,
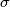 is the subcomplex with
is the subcomplex with  -simplices
-simplices 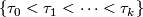 with
with 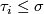 for all
for all  .
.
So we clearly have 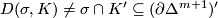 , since we have different conditions
, since we have different conditions 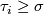 and
and 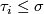 on the LHS and RHS respectively. This is solved by passing from
on the LHS and RHS respectively. This is solved by passing from 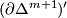 to
to 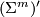 and replacing
and replacing 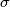 by
by 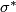 . Considered as subcomplexes of
. Considered as subcomplexes of 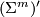 , we have:
, we have:
-
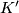 has
has  -simplices
-simplices 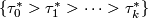 with
with 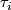 a simplex of
a simplex of  for each
for each  .
.
-
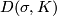 has
has  -simplices
-simplices 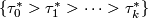 with
with 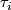 a simplex of
a simplex of  and
and 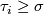 , equivalently
, equivalently 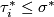 , for all
, for all  .
.
-
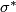 has
has  -simplices
-simplices 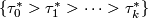 with
with 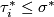 for all
for all  .
.
Hence,
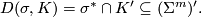
Remark 0.6.
Once we know that the dual cell decomposition of 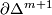 is actually a simplicial complex, in other words that
is actually a simplicial complex, in other words that 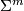 is a simplicial complex, then the argument is very simple and formal. The main geometric input to the argument is the special property of
is a simplicial complex, then the argument is very simple and formal. The main geometric input to the argument is the special property of 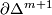 mentioned above, that
mentioned above, that 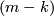 -simplices are precisely the
-simplices are precisely the  -fold intersections of
-fold intersections of  -simplices.
-simplices.