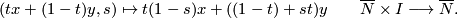Talk:Supplement II (Ex)
Definition 0.1.
Let  be a subcomplex of a simplicial complex
be a subcomplex of a simplicial complex  . The barycentric subdivision
. The barycentric subdivision 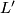 is the simplicial complex with
is the simplicial complex with  -simplices
-simplices 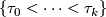 for
for 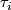 simplices of
simplices of  (totally-ordered by inclusion), and
(totally-ordered by inclusion), and 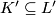 is the subcomplex whose
is the subcomplex whose  -simplices are
-simplices are 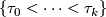 with
with 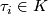 for all
for all  . The supplement
. The supplement 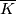 of
of  in
in  is the subcomplex
is the subcomplex 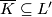 whose
whose  -simplices are
-simplices are 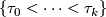 with
with 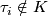 for all
for all  .
.
Definition 0.2.
For two spaces  and
and  , the join
, the join 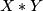 is by definition the quotient of
is by definition the quotient of 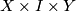 by the equivalence relation given by
by the equivalence relation given by
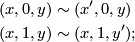
in other words 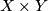 is collapsed to
is collapsed to  at the
at the  end and is collapsed to
end and is collapsed to  at the
at the  end. So formally its elements are
end. So formally its elements are 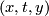 subject to this equivalence relation, but we will write them as formal sums
subject to this equivalence relation, but we will write them as formal sums 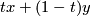 . (This notation indicates that when
. (This notation indicates that when 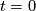 it doesn't matter what
it doesn't matter what  is and when
is and when 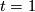 it doesn't matter what
it doesn't matter what  is.)
is.)
Construction 0.3.
We will embed 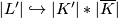 . First, we embed the subspaces
. First, we embed the subspaces 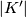 and
and 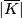 of
of 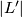 in the obvious way, i.e.
in the obvious way, i.e.
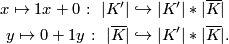
Let 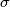 be a simplex of
be a simplex of 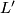 which is not in
which is not in 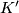 or
or 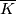 . So
. So
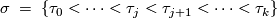
with 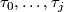 in
in  and
and 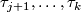 not in
not in  (
(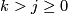 ). A point in
). A point in 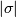 is given in barycentric coordinates by
is given in barycentric coordinates by
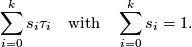
We define the embedding 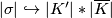 by the formula
by the formula
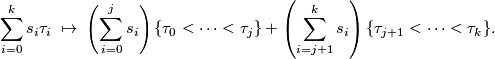
These embeddings of 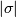 , for
, for 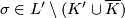 , together with the embeddings of
, together with the embeddings of 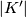 and
and 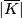 above, glue to give a well-defined embedding of
above, glue to give a well-defined embedding of 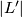 in
in 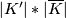 . (Since the definitions agree on overlaps.)
. (Since the definitions agree on overlaps.)
Deformation retracts 0.4. Now define
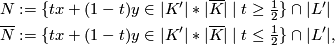
and note that
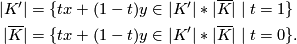
There is then an obvious deformation retraction
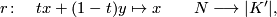
where 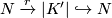 is homotopic to the identity via
is homotopic to the identity via
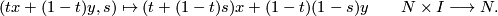
Similarly there is a deformation retraction
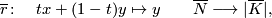
with 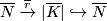 homotopic to the identity via
homotopic to the identity via