Talk:Structures on M x I (Ex)
Recall that an element of the simple structure set 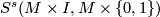 in the topological category is represented by a manifold
in the topological category is represented by a manifold  with boundary together with a simple homotopy equivalence
with boundary together with a simple homotopy equivalence 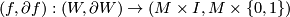 such that
such that 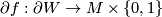 is a homeomorphism.
is a homeomorphism.
Two such objects 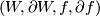 and
and 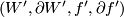 are equivalent in the structure set if there exists a homeomorphism
are equivalent in the structure set if there exists a homeomorphism 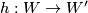 such that the maps commute up to simple homotopy equivalence
such that the maps commute up to simple homotopy equivalence 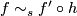 and commute strictly on the boundary
and commute strictly on the boundary 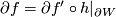 .
.
Take a representative 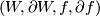 .
.
Since 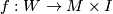 is a simple homotopy equivalence and
is a simple homotopy equivalence and  is an s-cobordism, the same is true for
is an s-cobordism, the same is true for  and by the s-cobordism theorem
and by the s-cobordism theorem  is homeomorphic to a cylinder
is homeomorphic to a cylinder  and every element of the structure set is represented by an element of the form
and every element of the structure set is represented by an element of the form 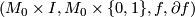 .
. 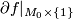 defines a homeomorphism
defines a homeomorphism 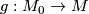 and precomposing the map
and precomposing the map 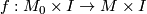 with
with 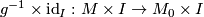 shows that every element of the structure set is even represented by an element of the form
shows that every element of the structure set is even represented by an element of the form 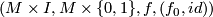 with
with  a self homeomorphism
a self homeomorphism 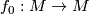 . Using this we will denote these representatives by
. Using this we will denote these representatives by 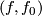 .
.
Define the map
![\displaystyle F:S^s(M\times I,M\times\{0,1\})\rightarrow \tilde \pi_0 \textup{SHomeo}_+(M), \quad [(f,f_0)] \mapsto[f_0].](/images/math/d/e/f/defda98b35087b57386334c1d3cc66c3.png)
To see that  is well defined assume that
is well defined assume that 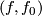 and
and 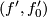 are equivalent. Then there exists a self homeomorphism
are equivalent. Then there exists a self homeomorphism  of
of 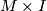 such that
such that 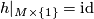 and
and 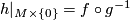 . So
. So 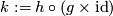 is a self homeomorphism of
is a self homeomorphism of 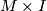 which is
which is  on one side and
on one side and  on the other side. So
on the other side. So  and
and  are pseudo-isotopic and
are pseudo-isotopic and  is well-defined.
is well-defined.
Take an element 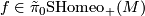 and choose a homotopy
and choose a homotopy  to the identity. This induces a map
to the identity. This induces a map 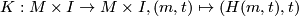 with
with 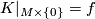 and
and 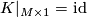 . So
. So ![[(K,f)]\in S^s(M\times I, M\times\{0,1\})](/images/math/3/3/1/3319211e39a669a139185b5fb91b5047.png) is a preimage of
is a preimage of  under
under  , i.e.
, i.e.  is surjective.
is surjective.
Since 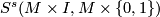 is abelian it remains to check that
is abelian it remains to check that  is a homomorphism of groups to show that
is a homomorphism of groups to show that  is abelian.
is abelian.
Let 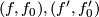 be two representatives as above.
be two representatives as above. 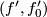 is in the structure set equivalent to
is in the structure set equivalent to 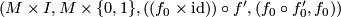 and the addition
and the addition 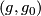 of
of 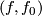 and
and 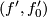 is defined by
gluing together
is defined by
gluing together 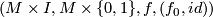 and
and 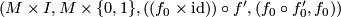 at the 1- respectively 0-boundary. So
at the 1- respectively 0-boundary. So 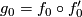 , which is the product of
, which is the product of 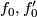 in
in  . So
. So  is a group homomorphism.
is a group homomorphism.
A proof of this exercise can also be found in [Wang1974].