Talk:Kernel formation (Ex)
From Manifold Atlas
The lens space 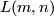 is a union of two solid tori glued along the boundary. The gluing diffeomorphism
is a union of two solid tori glued along the boundary. The gluing diffeomorphism 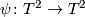 is such that
is such that 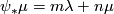 , where
, where  and
and  denote the longtitude and meridian of the solid torus.
From this Heegard decomposition we obtain the kernel formation
denote the longtitude and meridian of the solid torus.
From this Heegard decomposition we obtain the kernel formation
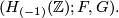
The first lagrangian  is spanned by the generator of
is spanned by the generator of 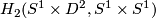 . This generator is exactly the meridian
. This generator is exactly the meridian  . The same argument shows, that the second lagrangian is generated by the image of the meridian of complementary torus
. The same argument shows, that the second lagrangian is generated by the image of the meridian of complementary torus 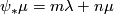 .
Certainly we have
.
Certainly we have 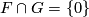 . Furthermore it is easy to see that the index of
. Furthermore it is easy to see that the index of 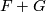 in
in 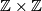 is equal to
is equal to  . Thus the kernel formation is trivial if and only if
. Thus the kernel formation is trivial if and only if 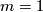 .
We have
.
We have 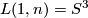 , thus we obtain trivial formations for
, thus we obtain trivial formations for  :
:
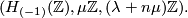
For 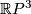 it is sufficient to notice that
it is sufficient to notice that 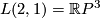 . Thus the associated formation is:
. Thus the associated formation is: