Talk:Inertia group I (Ex)
From Manifold Atlas
First observe, that instead of forming a connected sum 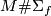 we may think of it as cutting a disc
we may think of it as cutting a disc 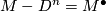 and glueing the disc back identifying boundary spheres via diffeomorphism
and glueing the disc back identifying boundary spheres via diffeomorphism 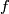 . By the theorem of Cerf definition of
. By the theorem of Cerf definition of 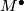 does not depend on the embedding
does not depend on the embedding 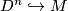 .
.
If 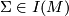 and
and 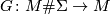 is a diffeomorphism, find a decomposition
is a diffeomorphism, find a decomposition 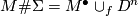 and set
and set 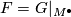 .
.
Conversely suppose that there exist a diffeomorphism 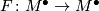 such that
such that 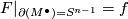 . Then glue a disc via identity to the source and target
. Then glue a disc via identity to the source and target 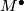 and extend
and extend 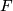 as identity. Composition of inclusion and
as identity. Composition of inclusion and 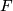 ,
, 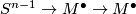 is equal to
is equal to 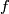 , hence (by definition) the target is equal to
, hence (by definition) the target is equal to 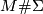 . This proves that
. This proves that 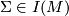 .
.
(Is the Cerfs thm properly applied?)