Self-maps of simply connected manifolds
Contents |
[edit] 1 Question
Let us call an oriented closed connected manifold flexible if it admits a self-map that has non-trivial degree (i.e., degree not equal to 1, 0, or -1).
Question 1.1. Do there exist closed simply connected manifolds (of non-zero dimension) that are not flexible?
Remark 1.2. In the following, for simplicity, we implicitly assume that all manifolds are of non-zero dimension.
[edit] 2 Examples and partial answers
[edit] 2.1 Examples of flexible manifolds
- Of course, all spheres are flexible.
- All odd-dimensional real projective spaces are flexible; all complex projective spaces are flexible.
- Products of flexible manifolds with oriented closed connected manifolds are flexible; in particular, tori are flexible.
- All closed simply connected 3-manifolds are flexible.
- All closed simply connected 4-manifolds are flexible [Duan&Wang2004, Corollary 2].
- ...
[edit] 2.2 Examples of manifolds that are not flexible
Notice that there are many oriented closed connected manifolds that are not flexible.
Example 2.1.
- All oriented closed connected manifolds with non-zero simplicial volume are not flexible (because the simplicial volume is functorial).
- This includes, for instance, oriented closed connected manifolds of non-positive sectional curvature. (More examples and explanations of these facts can be found on the page on simplicial volume.)
However, by a theorem of Gromov, the simplicial volume of closed simply connected manifolds is always zero. So the simplicial volume cannot be used to discover closed simply connected manifolds that are not flexible.
[edit] 3 Solution
This problem was in fact solved by Arkowitz and Lupton [Arkowitz&Lupton2000, Examples 5.1 & 5.2]: There do exist inflexible closed simply connected manifolds.
Arkowitz and Lupton give examples of simply connected rational Poincaré differential graded algebras, 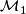 and
and 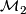 of dimensions 208 and 228. Both of these algebras have a finite set of homotopy classes of self-maps and so the corresponding rational Poincaré complexes are inflexible. They also indicate why the algebras
of dimensions 208 and 228. Both of these algebras have a finite set of homotopy classes of self-maps and so the corresponding rational Poincaré complexes are inflexible. They also indicate why the algebras 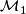 and
and 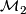 can be realised by closed simply connected manifolds
can be realised by closed simply connected manifolds  and
and 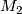 . It follows that the manifolds
. It follows that the manifolds  and
and 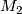 are inflexible.
are inflexible.
The realisation of 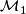 and
and 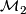 relies upon a theorem proven independently by Barge and Sullivan. A special case of this theorem is as follows:
relies upon a theorem proven independently by Barge and Sullivan. A special case of this theorem is as follows:
Theorem 3.1 [Barge1976, Theorem 1][Sullivan1977, Theorem 13.2].
Let 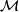 be a simply connected rational Poincaré differential graded algebra of dimension n. If either
be a simply connected rational Poincaré differential graded algebra of dimension n. If either
-
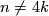 or
or
-
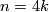 and the intersection form of
and the intersection form of 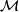 represents the trivial element of
represents the trivial element of 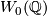 , the Witt group of
, the Witt group of 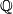 ,
,
then there is a closed simply connected smooth manifold  with rational homotopy type given by
with rational homotopy type given by 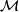 .
.
Remark 3.2.
Note that Arkowitz and Lupton [Arkowitz&Lupton2000] state that the theorem of Barge-Sullivan applies and do not give detailed arguments why 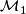 or
or 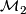 satisfy the hypotheses of Barge-Sullivan. See the discussion page for more information.
satisfy the hypotheses of Barge-Sullivan. See the discussion page for more information.
[edit] 4 References
- [Arkowitz&Lupton2000] M. Arkowitz and G. Lupton, Rational obstruction theory and rational homotopy sets, Math. Z. 235 (2000), no.3, 525–539. MR1800210 (2001h:55012) Zbl 0968.55005
- [Barge1976] J. Barge, Structures différentiables sur les types d'homotopie rationnelle simplement connexes, Ann. Sci. École Norm. Sup. (4) 9 (1976), no.4, 469–501. MR0440574 (55 #13448) Zbl 0348.57016
- [Duan&Wang2004] H. B. Duan and S. C. Wang, Non-zero degree maps between
 -manifolds, Acta Math. Sin. (Engl. Ser.) 20 (2004), no.1, 1–14. MR2056551 (2005b:57051) Zbl 1060.57018
-manifolds, Acta Math. Sin. (Engl. Ser.) 20 (2004), no.1, 1–14. MR2056551 (2005b:57051) Zbl 1060.57018
- [Sullivan1977] D. Sullivan, Infinitesimal computations in topology, Inst. Hautes Études Sci. Publ. Math. (1977), no.47, 269–331 (1978). MR0646078 (58 #31119) Zbl 0374.57002