Regensburg Surgery Blockseminar 2012: General information
The Regensburg surgery Blockseminar runs March 25 - 30 2012.
This page supports the scientific part of the meeting.
Contents |
[edit] 1 Introduction
The aim of this seminar is to give a detailed treatment of the smooth surgery exact sequence for manifolds of dimension 5 and higher and then to review extensions of this sequence to the piecewise linear and topological categories and to give a range of applications.
The main reference for the seminar is Wolfgang Lück's lecture notes, A basic introduction to surgery [Lück2001] but we will use various other sources.
[edit] 1.1 Prerequisites
The seminar will assume not go into the following important subjects:
- The general theory of smooth manifolds, submanifolds, normal bundles and tubular neighbourhoods: see e.g. [Milnor&Stasheff1974, Ch.11 & Ch 18].
- Participants are assumed to be familiar with the statement of the
 -cobordism theorem and hopefully it's proof: see [Milnor1965a].
-cobordism theorem and hopefully it's proof: see [Milnor1965a].
An excellent place to learn the essential ideas for surgery remains [Milnor1961], in particular the first four sections.
[edit] 2 Information for speakers
Each talk will run for 60 minutes with up to 15 minutes for questions.
The talks will be given using white-boards.
[edit] 2.1 Scientific guidelines
Where there is no single way to give a good talk, here are some suggestions:
- Identify the main result(s) of your talk.
- Aim to state your main results as quickly and as clearly as possible at the beginning of your talk: this may require leaving certain concepts to be fully explained in later in your talk.
- Where possible, illustrate the main results with clarifying examples and explain how they fit into the overall development of the seminar: i.e. indicate results from previous talks you build and/or results in future talks that build on your talk.
- Finally move onto the proof of your main results. Where possible, break the proof into a series of clearly stated lemmas and prove each lemma in turn. It is OK to skip the full proofs of technical or very difficult lemmas.
[edit] 3 Schedule
- The s-cobordism theorem I: [Lück2001, 1.1-1.3]; Farid Madani and Mihaela Pilca, Lecture notes
- The s-cobordism theorem II: [Lück2001, 1.3 & 1.4]; Regensburg
- The s-cobordism theorem III: [Lück2001, Ch.2]; Regensburg, Lecture notes
- Poincaré complexes: [Lück2001][3.1] L; Freiburg, Lecture notes
- Spherical fibrations and the normal Spivak fibration: [Lück2001, 3.2.2 & 3.2.3]; Freiburg, Lecture notes
- Normal maps and the Pontrjagin-Thom isomorphism: [Lück2001, 3.1 & 3.3]; Andreas Hermann and Michael Völkl, Lecture notes
- Surgery below the middle dimension: [Lück2001, 3.4]; Nicolas Ginoux and Carolina Neira-Jiménez, Lecture notes
- Intersections and self-intersections: [Lück2001, 4.1]; Regensburg
- Kernels and forms: [Lück2001, 4.2]; Filipp Levikov, Lecture notes
- Even dimensional surgery obstructions: [Lück2001, 4.3 & 4.4]; Edinburgh, Lecture notes
- Odd dimensional surgery obstructions: [Lück2001, 4.5 & 4.6]; Edinburgh
- Manifolds with boundary and simple surgery obstructions: [Lück2001, 4.7]; Bernd Ammann, Lecture notes
- The structure set and Wall realisation: [Lück2001, 5.1]; Münster, Lecture notes: part (a) Lecture notes: part (b)
- The smooth surgery exact sequence: [Lück2001, 5.2, 5.3 & 6.1]; Münster, Lecture notes
- Exotic spheres: [Lück2001, 6.1-6.5 & 6.7]; Sebastian Goette, Lecture notes
- The surgery exact sequence for TOP and PL: [Lück2001, 5.4 & 6.6]; Bonn, Lecture notes
- Manifolds homotopy equivalent to CPn: [Wall1999, 14C], [Madsen&Milgram1979, 8C]; Poznan, Lecture notes
- Fake Tori: [Wall1999, 15A]; Philipp Kühl and Anna Abczynski, Lecture notes
[edit] 3.1 Division of talks
Note that the program naturally splits into various groups of talks. The speakers from these groups should co-operate with one another both in learning the material and in decided how to organise its presentation.
- [A] Talks 1-3: The aims of these talks is to out-line the proof of the s-cobordism theorem assuming the audience is familiar with the proof of the h-cobordism theorem.
- [B] Talks 4-5: Here the key homotopy theoretic aspects of manifolds are identified: Poincar\'e duality and its surprising consequence: the existence of the Spivak normal fibration.
- [C] Talks 6-8: Working below the middle dimension we see how surgery and bordism are intimately related and how to make normal maps highly connected.
- [D] Talks 9-11: These talks present the heart of surgery: the surgery obstruction map arising out of the challenge of performing desired surgeries on middle-dimensional homotopy classes. Subtle topology and complex algebra and elegantly gathered into a powerful synthesis here.
- [E] Talks 12-14: Here we step back a little and see how to assemble all of the previous hard work into the succinct and powerful surgery exact sequence.
- [F] Talks 15-18: Now we give applications and show how to work with the surgery exact sequence. Starting with exotic spheres we see the spaces fundamental spaces
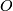 ,
,  ,
, 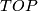 and
and  and their quotients, compute their homotopy groups and sometimes even their homotopy type. As a result we can calculate manifolds homotopy equivalent to
and their quotients, compute their homotopy groups and sometimes even their homotopy type. As a result we can calculate manifolds homotopy equivalent to  ,
, 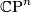 and
and 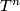 (in appropriate categories).
(in appropriate categories).
[edit] 4 References
- [Lück2001] W. Lück, A basic introduction to surgery theory, 9 (2001), 1–224. Available from the author's homepage. MR1937016 (2004a:57041) Zbl 1045.57020
- [Madsen&Milgram1979] I. Madsen and R. J. Milgram, The classifying spaces for surgery and cobordism of manifolds, Princeton University Press, Princeton, N.J., 1979. MR548575 (81b:57014) Zbl 0446.57002
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Milnor1961] J. Milnor, A procedure for killing homotopy groups of differentiable manifolds, Proc. Sympos. Pure Math, Vol. III (1961), 39–55. MR0130696 (24 #A556) Zbl 0118.18601
- [Milnor1965a] J. Milnor, Lectures on the
 -cobordism theorem, Princeton University Press, Princeton, N.J., 1965. MR0190942 (32 #8352) Zbl 0161.20302
-cobordism theorem, Princeton University Press, Princeton, N.J., 1965. MR0190942 (32 #8352) Zbl 0161.20302
- [Wall1999] C. T. C. Wall, Surgery on compact manifolds, American Mathematical Society, Providence, RI, 1999. MR1687388 (2000a:57089) Zbl 0935.57003