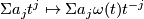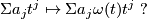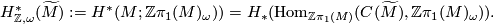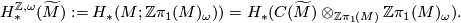Poincaré duality III (Ex)
From Manifold Atlas
Let  be
be
-
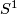
-
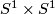
-
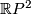
-
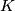 the Klein bottle
the Klein bottle
Consider all possible representations 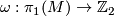 . Compute
. Compute
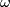 do we get Poincaré Duality
do we get Poincaré Duality ![\displaystyle [M]\cap - : \left\{ \begin{array}{c} H^{k}_{\mathbb{Z},\omega}(\widetilde{M}) \to H_{\dim M -k}(\widetilde{M}) \\ H^{k}(\widetilde{M}) \to H^{\mathbb{Z},\omega}_{\dim M -k}(\widetilde{M}) \end{array}\right. ?](/images/math/c/e/c/cec5b1c940f67421c9679f24553cd6a4.png)
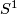 , why is the correct involution for Poincaré Duality
, why is the correct involution for Poincaré Duality