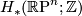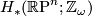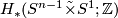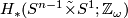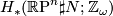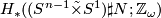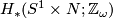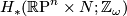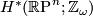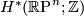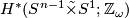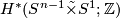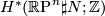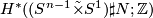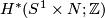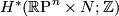Poincaré duality (Ex)
From Manifold Atlas
Let 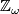 the local coefficient system of
the local coefficient system of 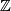 twisted the orientation character
twisted the orientation character 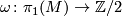 of a compact manifold
of a compact manifold  , let
, let 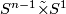 denote the total space of the non-trivial linear sphere bundle over
denote the total space of the non-trivial linear sphere bundle over 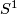 and let
and let 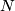 be a closed simply connected manifold.
be a closed simply connected manifold.
Determine the following homology groups (in terms of 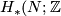 where appropriate):
where appropriate):
Determine the following cohomology groups and verify Poincaré duality using the homology computations above:
Here are some helpful references for the definitions involved: [Davis&Kirk2001, Ch 5] [Wall1967a, Chapter 1]