KO-Characteristic classes
From Manifold Atlas
|
This page has not been refereed. The information given here might be incomplete or provisional. |
[edit] 1 KO-Pontryagin classes
The KO-Pontryagin classes 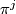 for oriented vector bundles, i.e. in
for oriented vector bundles, i.e. in 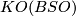 are defined by setting
are defined by setting
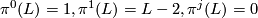 for
for 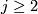 for complex line bundles L and then requiring naturality and
for complex line bundles L and then requiring naturality and
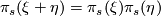 where
where 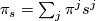 .
Here
.
Here  and
and 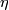 are oriented bundles.
are oriented bundles.
In fact, these properties determine 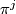 because the group
because the group 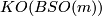 injects into
injects into ![K(BT^{[m/2]})](/images/math/3/6/4/364dfbae4b2336e2bafa5ef956102a4f.png) under the
complexification of the map which is induced by the restriction to the maximal torus
under the
complexification of the map which is induced by the restriction to the maximal torus ![T^{[m/2]}](/images/math/f/6/2/f62a2f55a50b2ecc510a731975035028.png) (compare [Anderson&Brown&Peterson1966a]).
(compare [Anderson&Brown&Peterson1966a]).
[edit] 2 References
- [Anderson&Brown&Peterson1966a] D. W. Anderson, E. H. Brown and F. P. Peterson,
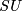 -cobordism,
-cobordism, 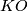 -characteristic numbers, and the Kervaire invariant, Ann. of Math. (2) 83 (1966), 54–67. MR0189043 (32 #6470) Zbl 0137.42802
-characteristic numbers, and the Kervaire invariant, Ann. of Math. (2) 83 (1966), 54–67. MR0189043 (32 #6470) Zbl 0137.42802