Hilbert manifold
|
An earlier version of this page was published in the Definitions section of the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 14:51, 13 February 2014 and the changes since publication. |
|
The user responsible for this page is Lennart Meier. No other user may edit this page at present. |
Contents |
1 Introduction and Definition
Even if one is interested only in finite-dimensional manifolds, the need for infinite-dimensional manifolds sometimes arises. For example, one approach to study closed geodesics on a manifold is to use Morse theory on its (free) loop space; while for some purposes it is enough to work with finite-dimensional approximations, it is helpful for some finer aspects of the theory to use models of the free loop space that are infinite-dimensional manifolds. The use of Morse theory in an infinite-dimensional context is even more important for other (partial) differential equations like those occuring in the theory of minimal surfaces and the Yang-Mills equations. Morse theory for infinite dimensional manifolds was developed by Palais and Smale ([Palais&Smale1964], [Palais1963]).
While there is up to isomorphism only one vector space of every finite dimension, there are many different kinds of infinite-dimensional topological vector spaces one can choose. Modeling spaces on Fréchet spaces gives the notion of Fréchet manifolds, modelling on Banach spaces gives Banach manifolds, modelling on the Hilbert cube (the countably infinite product of intervals) gives Hilbert cube manifolds. We will stick to Hilbert manifolds (which are not directly related to Hilbert cube manifolds).
Definition 1.1.
Let  be the (up to isomorphism unique) separable Hilbert space of infinite dimension. Then a Hilbert manifold is a separable metrizable space such that every point has a neighborhood that is homeomorphic to an open subset of
be the (up to isomorphism unique) separable Hilbert space of infinite dimension. Then a Hilbert manifold is a separable metrizable space such that every point has a neighborhood that is homeomorphic to an open subset of  .
.
Some authors have slightly different definitions, leaving out the metrizability or the separability condition. Note that metrizability always implies paracompactness and here also the converse is true. Being metrizable and separable is in this context also equivalent to being second countable and Hausdorff by Uryson's metrization theorem (see also [Eells1966, 4(A)]).
Note that every separable Frechet space is homeomorphic to the separable Hilbert space (see [Anderson&Bing1968]). Thus, the structure of a topological Hilbert manifold is not different from that of a topological Frechet manifold; only in the differentiable case differences show up. A 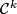 -structure for
-structure for 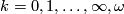 can be defined as usual as an equivalence class of atlases whose chart transition maps are of class
can be defined as usual as an equivalence class of atlases whose chart transition maps are of class 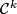 . Here,
. Here, 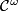 stands for analytic functions. The tangent bundle of a Hilbert manifold can also be defined as usual for
stands for analytic functions. The tangent bundle of a Hilbert manifold can also be defined as usual for 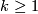 and is a Hilbert space bundle with structure group
and is a Hilbert space bundle with structure group 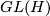 with the norm topology (see [Lang1995], II.1 and III.2).
with the norm topology (see [Lang1995], II.1 and III.2).
A submanifold of a Hilbert manifold  is a subset
is a subset  such that for every point
such that for every point 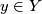 there is an open neighborhood
there is an open neighborhood  of
of  in
in  and a homeomorphism
and a homeomorphism 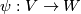 to an open subset
to an open subset  such that
such that 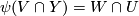 for
for  a closed linear subspace of
a closed linear subspace of  .
.
2 Properties
2.1 Basic Differential Topology
Many basic theorems of differential topology carry over from the finite dimensional situation to the Hilbert (and even Banach) setting with little change. For example, every smooth submanifold of a smooth Hilbert manifold has a tubular neighborhood, unique up to isotopy (see [Lang1995] IV.5-6 and also [Ramras2008] for the non-closed case). Also, every Hilbert manifold can be embedded as a closed submanifold into the standard Hilbert space ([Kuiper&Terpstra-Keppler1970]). However, in statements involving maps between manifolds, one often has to restrict consideration to Fredholm maps, i.e. maps whose differential at every point has closed image and finite-dimensional kernel and cokernel. The reason for this is that Sard's lemma holds for Fredholm maps, but not in general (see [Smale1965] and [Bonic1966]). The precise statement is:
Theorem 2.1 [Smale1965] .
Let 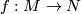 be a smooth Fredholm map between Hilbert manifolds. Then its set of regular values is the intersection of countably many sets with dense interior.
be a smooth Fredholm map between Hilbert manifolds. Then its set of regular values is the intersection of countably many sets with dense interior.
2.2 Homotopy Theory
On the other hand, every countable, locally finite simplicial complex is homotopy equivalent to an open subset of the standard Hilbert space. Thus, the homotopy classification of Hilbert manifolds is equivalent to that of countable, locally finite simplicial complexes or, equivalently, countable CW-complexes (see [Burghelea&Kuiper1969], Section 10).
2.3 Specialties of Infinite Dimension
While proofs are often harder in infinite dimensions, some things are true for Hilbert manifolds that could not be hoped for in finite dimensions.
 can be embedded onto an open subset of the model Hilbert space.
can be embedded onto an open subset of the model Hilbert space.Indeed, Burghelea and Kuiper show this result under the assumption of the existence of a Morse function and Moulis shows the existence of a Morse function on an open subset of the standard Hilbert space.
Thus, the category of topological Hilbert manifolds with homeomorphisms up to isotopy and the category of smooth Hilbert manifolds with diffeomorphisms up to isotopy are equivalent.
The situation is different for complex analytic structures. These always exist, but are not unique. Indeed, there are infinitely many nonequivalent complex analytic structures on every Hilbert manifold (see [Burghelea&Duma1971]).
Although Sard's Theorem does not hold in full generality, note that we have also the following theorem:
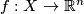 from a Hilbert manifold can be arbitrary closely approximated by a smooth map
from a Hilbert manifold can be arbitrary closely approximated by a smooth map 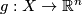 that has no critical points.
that has no critical points.3 Examples
 of a separable Hilbert space
of a separable Hilbert space  is a Hilbert manifold with a single global chart given by the inclusion into
is a Hilbert manifold with a single global chart given by the inclusion into  . Up to diffeomorphisms, every Hilbert manifold is of this form by [Henderson1970].
. Up to diffeomorphisms, every Hilbert manifold is of this form by [Henderson1970].Example 3.3. Mapping spaces between manifolds can often be viewed as Hilbert manifolds if one considers only maps of suitable Sobolev class. Set 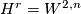 to be the Sobolev class of
to be the Sobolev class of  -functions which are
-functions which are  -fold weakly differentiable in
-fold weakly differentiable in  . Let now
. Let now  be an
be an  -dimensional compact smooth manifold,
-dimensional compact smooth manifold,  be an arbitrary smooth finite-dimensional or Hilbert manifold and
be an arbitrary smooth finite-dimensional or Hilbert manifold and 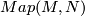 be the space of continuous maps with the compact-open topology. Then the subspace
be the space of continuous maps with the compact-open topology. Then the subspace 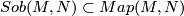 of functions of Sobolev type
of functions of Sobolev type 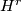 for
for 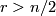 can be given the structure of a smooth Hilbert manifold ([Eells1966, 6(D)]). This inclusion is a homotopy equivalence ([Eells1966, 6(E)]). In particular,
can be given the structure of a smooth Hilbert manifold ([Eells1966, 6(D)]). This inclusion is a homotopy equivalence ([Eells1966, 6(E)]). In particular, 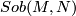 is diffeomorphic to any other Hilbert manifold homotopy equivalent to
is diffeomorphic to any other Hilbert manifold homotopy equivalent to 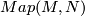 and therefore its diffeomorphism type depends only on the homotopy type of
and therefore its diffeomorphism type depends only on the homotopy type of  and
and  . Hilbert manifold models for mapping spaces (in particular, free loop spaces) have been used, for example, in the study of closed geodesics ([Klingenberg1995], [Klingenberg1978]), string topology ([Chataur2005], [Meier2011]) and fluid dynamics ([Ebin&Marsden1970]).
. Hilbert manifold models for mapping spaces (in particular, free loop spaces) have been used, for example, in the study of closed geodesics ([Klingenberg1995], [Klingenberg1978]), string topology ([Chataur2005], [Meier2011]) and fluid dynamics ([Ebin&Marsden1970]).
4 References
- [Anderson&Bing1968] R. D. Anderson and R. H. Bing, A complete elementary proof that Hilbert space is homeomorphic to the countable infinite product of lines, Bull. Amer. Math. Soc. 74 (1968), 771–792. MR0230284 (37 #5847) Zbl 0189.12402
- [Azagra&Cepedello Boiso2004] D. Azagra and M. Cepedello Boiso, Uniform approximation of continuous mappings by smooth mappings with no critical points on Hilbert manifolds, Duke Math. J. 124 (2004), no.1, 47–66. MR2072211 (2005h:57037) Zbl 1060.57015
- [Bonic1966] R. Bonic, A note on Sard's theorem in Banach spaces, Proc. Amer. Math. Soc. 17 (1966), 1218. MR0198493 (33 #6648) Zbl 0173.16904
- [Burghelea&Duma1971] D. Burghelea and A. Duma, Analytic complex structures on Hilbert manifolds, J. Differential Geometry 5 (1971), 371–381. MR0292115 (45 #1202) Zbl 0226.58004
- [Burghelea&Henderson1970] D. Burghelea and D. Henderson, Smoothings and homeomorphisms for Hilbert manifolds, Bull. Amer. Math. Soc. 76 (1970), 1261–1265. MR0283827 (44 #1057) Zbl 0211.56004
- [Burghelea&Kuiper1969] D. Burghelea and N. H. Kuiper, Hilbert manifolds, Ann. of Math. (2) 90 (1969), 379–417. MR0253374 (40 #6589) Zbl 0195.53501
- [Burghelea1970] D. Burghelea, Diffeomorphisms for Hilbert manifolds and handle decomposition, Bull. Amer. Math. Soc. 76 (1970), 352–357. MR0258065 (41 #2712) Zbl 0197.20603
- [Chataur2005] D. Chataur, A bordism approach to string topology, Int. Math. Res. Not. (2005), no.46, 2829–2875. MR2180465 (2007b:55009) Zbl 1086.55004
- [Ebin&Marsden1970] D. G. Ebin and J. Marsden, Groups of diffeomorphisms and the motion of an incompressible fluid. , Ann. of Math. (2) 92 (1970), 102–163. MR0271984 (42 #6865) Zbl 0286.76001
- [Eells&Elworthy1970] J. Eells and K. D. Elworthy, Open embeddings of certain Banach manifolds, Ann. of Math. (2) 91 (1970), 465–485. MR0263120 (41 #7725) Zbl 0198.28804
- [Eells1966] J. Eells, A setting for global analysis, Bull. Amer. Math. Soc. 72 (1966), 751–807. MR0203742 (34 #3590) Zbl 0191.44101
- [Henderson1970] D. W. Henderson, Infinite-dimensional manifolds are open subsets of Hilbert space, Topology 9 (1970), 25–33. MR0250342 (40 #3581) Zbl 0167.51904
- [Klingenberg1978] W. Klingenberg, Lectures on closed geodesics, Springer-Verlag, 1978. MR0478069 (57 #17563) Zbl 0517.58004
- [Klingenberg1995] W. P. A. Klingenberg, Riemannian geometry, Walter de Gruyter & Co., 1995. MR1330918 (95m:53003) Zbl 1073.53006
- [Kuiper&Terpstra-Keppler1970] N. H. Kuiper and B. Terpstra-Keppler, Differentiable closed embeddings of Banach manifolds, Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer (1970), 118–125. MR0264709 (41 #9300) Zbl 0193.24001
- [Kuiper1965] N. H. Kuiper, The homotopy type of the unitary group of Hilbert space, Topology 3 (1965), 19–30. MR0179792 (31 #4034) Zbl 0129.38901
- [Lang1995] S. Lang, Differential and Riemannian manifolds, Springer-Verlag, 1995. MR1335233 (96d:53001) Zbl 0824.58003
- [Meier2011] L. Meier, Spectral sequences in string topology, Algebr. Geom. Topol. 11 (2011), no.5, 2829–2860. MR2846913 () Zbl 1227.55007
- [Moulis1968] N. Moulis, Sur les variétés Hilbertiennes et les fonctions non dégénérées, Nederl. Akad. Wetensch. Proc. Ser. A 71 = Indag. Math. 30 (1968), 497–511. MR0254876 (40 #8083) Zbl 0167.50204
- [Palais&Smale1964] R. S. Palais and S. Smale, A generalized Morse theory, Bull. Amer. Math. Soc. 70 (1964), 165–172. MR0158411 (28 #1634) Zbl 0119.09201
- [Palais1963] R. S. Palais, Morse theory on Hilbert manifolds, Topology 2 (1963), 299–340. MR0158410 (28 #1633) Zbl 0122.10702
- [Palais1966] R. S. Palais, Homotopy theory of infinite dimensional manifolds, Topology 5 (1966), 1–16. MR0189028 (32 #6455) Zbl 0138.18302
- [Ramras2008] D. A. Ramras, The Yang-Mills stratification for surfaces revisited, (2008). Available at the arXiv:0805.2587.
- [Smale1965] S. Smale, An infinite dimensional version of Sard's theorem, Amer. J. Math. 87 (1965), 861–866. MR0185604 (32 #3067) Zbl 0143.35301
5 External links
- The Wikipedia page about Hilbert manifolds