Handlebody decompositions of bordisms (Ex)
In the following we use the notation of [Lück2001, Section 1.1]. In particular, if  is an
is an  -manifold with boundary component
-manifold with boundary component 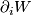 and
and
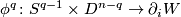
is an embedding then 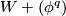 denotes the manifold of obtained from
denotes the manifold of obtained from  by attaching a
by attaching a  -handle along
-handle along 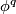 :
:
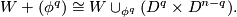
Exercise 0.1.
Let 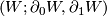 be an
be an  -dimensional cobordism, and suppose that, relative to
-dimensional cobordism, and suppose that, relative to 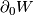 , we have
, we have
![\displaystyle W \cong \bigl(\partial_0 W \times [0,1] \bigr) + \sum_{i=1}^{p_0} (\phi^0_i) + \ldots + \sum_{i=1}^{p_n} (\phi^n_i).](/images/math/c/f/1/cf143453d1e27a4938c6c45c408229a7.png)
Show that there is another diffeomorphism, relative to 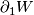 , which is of the following form:
, which is of the following form:
![\displaystyle W \cong \bigl( \partial_1 W \times [0,1] \bigr) + \sum_{i=1}^{p_n} (\psi^0_i) + \ldots + \sum_{i=1}^{p_0} (\psi^n_i).](/images/math/a/c/d/acdf79af6c159ecafee5029b2c187ba4.png)
The important part is that for each  -handle in the first handlebody decomposition, we have an
-handle in the first handlebody decomposition, we have an 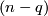 -handle in the second, dual handlebody decomposition.
-handle in the second, dual handlebody decomposition.
Comment 0.2. If one approaches this exercise using Morse functions (and their relation to handlebody decompositions), the above is almost trivial (Question: Why?). The actual intention of this exercise is to go through the details of the rather direct approach outlined in [Lück2001, pp.17-18]. While this is a bit tedious, it provides a good opportunity to get more familiar with handlebody attachments and the like.
Exercise 0.3.
Let  be an
be an  -dimensional manifold whose boundary
-dimensional manifold whose boundary 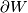 is the disjoint sum
is the disjoint sum 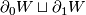 and let
and let 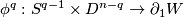 be a trivial embedding i.e. an embedding which is given by the restriction of an embedding of the disk
be a trivial embedding i.e. an embedding which is given by the restriction of an embedding of the disk 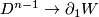 via a fixed standard embedding
via a fixed standard embedding 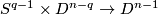 .
.
Show that there exists an embedding 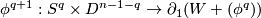 , such that
, such that 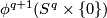 meets the transverse sphere of the handle
meets the transverse sphere of the handle 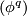 transversally in exactly one point. Conclude by the Cancellation Lemma [Lück2001, Lemma 1.12] that
transversally in exactly one point. Conclude by the Cancellation Lemma [Lück2001, Lemma 1.12] that  and
and 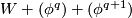 are diffeomorphic relative to
are diffeomorphic relative to 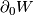 .
.
Exercise 0.4.
Let 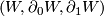 be an h-cobordism with
be an h-cobordism with 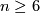 , which is written as follows:
, which is written as follows:
![\displaystyle W\cong \bigl(\partial_0W\times[0,1] \bigr) + \underset{i=1}{\overset{p_2}{\sum}}(\phi_i^2)+\cdots +\underset{i=1}{\overset{p_n}{\sum}}(\phi_i^n).](/images/math/1/7/0/170e3e4624440a2f1dc5f8e99744aad7.png)
For 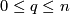 let
let 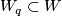 be the result of attaching all the
be the result of attaching all the  -handles of
-handles of  to
to ![\partial_0W \times [0, 1]](/images/math/0/3/a/03a8e7dcf5239cab3e901c27535f236d.png) for
for 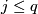 . Fix
. Fix 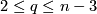 and assume that
and assume that 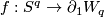 is an embedding which meets the transverse sphere of
is an embedding which meets the transverse sphere of 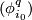 transversally in exactly one point and is disjoint from the transverse spheres of the handles
transversally in exactly one point and is disjoint from the transverse spheres of the handles 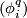 for
for 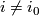 . Show that there is
. Show that there is 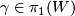 with
with
![\displaystyle [\tilde{f}]=\pm\gamma\cdot[\phi^q_{i_0}]\in H_q(\widetilde{W}_q, \widetilde{W}_{q-1})\cong \pi_q(\widetilde{W}_q, \widetilde{W}_{q-1})](/images/math/d/2/0/d2038afbca10cbc74ee55b4b2cdac8fe.png)
The exercises and comments on this page were sent by Alex Koenen, Farid Madani, Mihaela Pilca and Arkadi Schelling.