Extending functors on the category of manifolds and submersions
|
The users responsible for this page are: Matthias Kreck, Haggai Tene. No other users may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
There exist natural constructions of contravariant functors on the category of smooth manifolds and submersions which one would like to extend to a functor for all smooth maps. For example, if one assigns to a smooth manifold  the groupoid whose objects are pairs
the groupoid whose objects are pairs 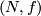 of smooth proper maps
of smooth proper maps 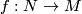 , and morphism are diffeomorphism
, and morphism are diffeomorphism 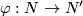 commuting with
commuting with  and
and  resp., one has for a submersion
resp., one has for a submersion 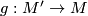 an induced map by the pullback construction. If one passes to cobordism classes of pairs
an induced map by the pullback construction. If one passes to cobordism classes of pairs 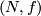 one obtains groups and transversality can be used to define induced maps for arbitrary maps
one obtains groups and transversality can be used to define induced maps for arbitrary maps 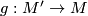 . This is Quillen's geometric construction of cobordism theory as a cohomology theory on the category of manifolds and all smooth maps.
. This is Quillen's geometric construction of cobordism theory as a cohomology theory on the category of manifolds and all smooth maps.
Let  be a compact Lie group. Consider the corresponding functors, where all manifolds are endowed with a smooth
be a compact Lie group. Consider the corresponding functors, where all manifolds are endowed with a smooth  action and all maps are equivariant. Again, cobordism classes form a group, but in this case the transversality theorem does not hold and so the question comes up how to construct induced maps. A similar problem with transversality occurs for maps between infinite dimensional manifolds.
action and all maps are equivariant. Again, cobordism classes form a group, but in this case the transversality theorem does not hold and so the question comes up how to construct induced maps. A similar problem with transversality occurs for maps between infinite dimensional manifolds.
In this note we explain how to overcome this difficulty by extending functors with certain properties, defined on the category of smooth  -manifolds and equivariant submersions, to functors, where induced maps are defined for all smooth equivariant maps.
-manifolds and equivariant submersions, to functors, where induced maps are defined for all smooth equivariant maps.
Contents |
1 Introduction
Let  be a compact Lie group. Given a contravariant homotopy functor
be a compact Lie group. Given a contravariant homotopy functor 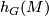 from the category of smooth
from the category of smooth  -manifolds (either finite dimensional or Hilbert manifolds) and morphisms which are equivariant submersions to the category of abelian groups we would like to construct an extension of induced maps for arbitrary equivariant smooth maps. By a homotopy functor we mean that if we have a homotopy through submersions, then the induced maps agree. We also want the extended functor to be a homotopy functor on all smooth maps.
-manifolds (either finite dimensional or Hilbert manifolds) and morphisms which are equivariant submersions to the category of abelian groups we would like to construct an extension of induced maps for arbitrary equivariant smooth maps. By a homotopy functor we mean that if we have a homotopy through submersions, then the induced maps agree. We also want the extended functor to be a homotopy functor on all smooth maps.
The following is a necessary condition:
Condition: If 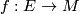 is a smooth equivariant vector bundle then
is a smooth equivariant vector bundle then 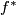 is an isomorphism.
is an isomorphism.
Theorem 1.1. Let 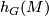 be a contravariant homotopy functor from the category of smooth
be a contravariant homotopy functor from the category of smooth  -manifolds (either finite dimensional or Hilbert manifolds) and morphisms which are equivariant submersions, to the category of abelian groups such that the condition above is fulfilled. Then there is a unique extension to a homotopy functor on all equivariant smooth maps.
If
-manifolds (either finite dimensional or Hilbert manifolds) and morphisms which are equivariant submersions, to the category of abelian groups such that the condition above is fulfilled. Then there is a unique extension to a homotopy functor on all equivariant smooth maps.
If 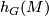 is a graded abelian group together with a natural Meyer-Vietoris sequence for every equivariant open covering
is a graded abelian group together with a natural Meyer-Vietoris sequence for every equivariant open covering 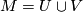 (a cohomology theory on the category of smooth manifolds and submersions), then the extension to the category of smooth manifolds and all smooth maps is again a cohomology theory: The Meyer-Vietoris sequence is again natural.
(a cohomology theory on the category of smooth manifolds and submersions), then the extension to the category of smooth manifolds and all smooth maps is again a cohomology theory: The Meyer-Vietoris sequence is again natural.
2 The construction
The proof is given by factoring an arbitrary smooth map through the composition of an embedding and a submersion to construct the extension in a unique way. The main thing left to be shown is functoriality. We prepare the construction of the extension with considerations concerning equivariant tubular neighborhoods.
Lemma 2.1. Every equivariant closed smooth embedding has an equivariant tubular neighborhood, which is unique up to homotopy through submersions.
Proof. Tubular neighborhoods can be constructed as in the finite dimensional setting. This is carried out in [Lang1999] using the concept of sprays. Instead one can use a Riemannian metric. From both data one gets the exponential map, which is a diffeomorphism on a small neighborhood of the zero section of the normal bundle to its image. Then one uses partition of unity to construct a diffeomorphism by shrinking the normal bundle to the open neighborhood. All this works equivariantly for compact Lie group actions. The only difference is that one considers an equivariant Riemannian metric which one obtains by averaging a non-equivariant Riemannian metric. Then the exponential map is automatically equivariant. Similarly, the shrinking construction works equivariantly by using an equivariant partition of unity, which again can be obtained from a non-equivariant partition of unity by averaging. The uniqueness is obtained by using a relative equivariant tubular neighborhood

Given an equivariant closed smooth embedding 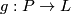 with an equivariant tubular neighborhood
with an equivariant tubular neighborhood 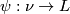 and projection map
and projection map 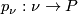 , denote
, denote 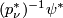 by
by 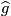 . Since equivariant tubular neighborhoods are unique up to homotopy through submersions
. Since equivariant tubular neighborhoods are unique up to homotopy through submersions 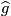 is independent of this choice.
is independent of this choice.
With this we define induced maps for an arbitrary equivariant smooth map 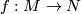 as follows. First, we factor
as follows. First, we factor  as the composition of the closed embedding
as the composition of the closed embedding 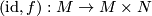 and the projection
and the projection 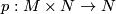 . Then we define
. Then we define
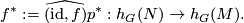
We have to show:
1) 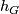 coincides with the previously defined functor for equivariant submersions.
coincides with the previously defined functor for equivariant submersions.
2) 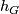 is a homotopy functor from the category of smooth (Hilbert) G-manifolds and equivariant smooth maps.
is a homotopy functor from the category of smooth (Hilbert) G-manifolds and equivariant smooth maps.
Proposition 2.2. The definition of induced maps coincides with the previous definition for submersions.
Proof.
Let 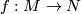 be an equivariant submersion. We need to show that
be an equivariant submersion. We need to show that 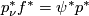 , which is equivalent to showing that
, which is equivalent to showing that 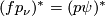 by functoriality for submersions. This holds since
by functoriality for submersions. This holds since 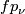 is homotopic to
is homotopic to 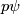 via submersions. A homotopy is given by mapping
via submersions. A homotopy is given by mapping 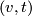 to
to 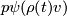 , where
, where ![\rho : [0,1] \to [0,1]](/images/math/2/6/a/26a3fc070aa9234ac0ef300059f5f8a6.png) is a smooth map, which is
is a smooth map, which is  near
near  and
and  near
near  . It is a homotopy via submersions, since for
. It is a homotopy via submersions, since for 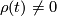 one uses that
one uses that 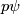 is a submersion and for
is a submersion and for 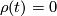 one uses that
one uses that 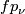 is a submersion.
is a submersion.

It is clear from the construction that this extension is unique. The fact that it depends only on the homotopy class of the map follows from the fact that if  is homotopic to
is homotopic to  then
then 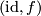 is isotopic to
is isotopic to 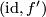 .
.
We are left to show functoriality. This is done in few steps.
Lemma 2.3. Given a pullback square
![\displaystyle \xymatrix{ M \ar[d]^{p} \ar[r]^{f} & N\ar[d]^{p'} \\ M'\ar[r]^{f'} & N',\\}](/images/math/c/0/0/c009abcadb25a272cb4a362530f87ce5.png)
where  is an equivariant closed smooth embedding and
is an equivariant closed smooth embedding and 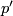 is an equivariant submersion. Then
is an equivariant submersion. Then 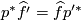 .
.
Proof.
Since this is a pullback square,  is an equivariant closed smooth embedding and
is an equivariant closed smooth embedding and  is an equivariant submersion, therefore, all induced maps are defined.
is an equivariant submersion, therefore, all induced maps are defined.
In Theorem 6.7 in [Hirsch1976] the following was proven for non-equivariant maps. In the diagram above, if 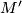 is compact, then suppose given tubular neighborhoods
is compact, then suppose given tubular neighborhoods 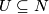 of
of  and
and 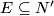 of
of 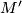 . Let
. Let 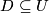 be a disk bundle such that
be a disk bundle such that 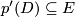 , then one can approximate
, then one can approximate 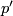 by
by 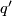 , via a homotopy
, via a homotopy 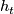 , such that
, such that 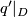 is a vector bundle map,
is a vector bundle map, 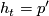 on
on 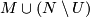 for
for 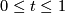 and
and 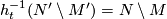 for
for 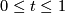 .
.
The same argument works for non-compact 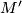 if one replaces
if one replaces 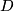 by a subbundle
by a subbundle 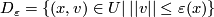 , for some map
, for some map 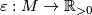 . In order to have a disk bundle as in Hirsch's Theorem, one has to renormalize the metric. In addition, by taking equivariant tubular neighbourhoods and an equivariant map
. In order to have a disk bundle as in Hirsch's Theorem, one has to renormalize the metric. In addition, by taking equivariant tubular neighbourhoods and an equivariant map  (which can be constructed, since
(which can be constructed, since  is compact), one obtains the same result in the equivariant setting. Notice, that since the subspace of all submersions is open in the space of all maps, one can choose
is compact), one obtains the same result in the equivariant setting. Notice, that since the subspace of all submersions is open in the space of all maps, one can choose 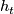 such that it a submersion for all
such that it a submersion for all 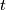 .
Since all induced maps remain unchanged along the homotopy we may assume with no loss of generality that
.
Since all induced maps remain unchanged along the homotopy we may assume with no loss of generality that 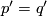 . Hence, we obtain the following commutative diagram where all maps are submersions:
. Hence, we obtain the following commutative diagram where all maps are submersions:
![\displaystyle \xymatrix{ M \ar@{->>}[d]^{p} & \nu \ar@{->>}[d]^{p''} \ar[r]^{\psi} \ar@{->>}[l]_{p_\nu}& N \ar@{->>}[d]^{p'} \\ M' &\nu' \ar[r]^{\psi '} \ar@{->>}[l]_{p_\nu '}& N' \\}](/images/math/b/8/a/b8a0628771eb76326ef8803ba5cb3382.png)
This proves the lemma since the induced maps for submersions are functorial.

Lemma 2.4.
Let 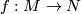 and
and 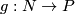 be equivariant closed smooth embeddings, then
be equivariant closed smooth embeddings, then
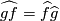 .
.
Proof.
Denote by 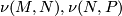 and
and 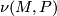 the normal bundles of the image of
the normal bundles of the image of 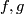 and
and 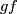 respectively. We have the following commutative diagram
respectively. We have the following commutative diagram
![\displaystyle \xymatrix{ & \nu_{(M,P)}\ar[d]^{\exists \cong} \ar[dr] \ar[drr] \ar[ddl]&& \\ &U\ar[r] \ar[d]&\nu_{(N,P)} \ar[r] \ar[d]&P\\ M&\nu_{(M,N)}\ar[r] \ar[l]& N&\\}](/images/math/d/c/9/dc97ea70045610c1792874087455b74f.png)
where  is the pullback of the square. Since all maps are submersions the result follows from the commutativity and the naturality for induced maps for submersions.
is the pullback of the square. Since all maps are submersions the result follows from the commutativity and the naturality for induced maps for submersions.

Lemma 2.5.
If 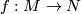 is an equivariant closed smooth embedding then
is an equivariant closed smooth embedding then 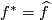 .
.
Proof. Look at the following commutative diagram:
![\displaystyle \xymatrix{ M \ar@{^{(}->}[r]^{(\id,\id)} \ar[dr]^{\id} & M\times M \ar[d]^{p} \ar@{^{(}->}[r]^{(\id,f)} & M\times N \ar[d]^{p} \\ & M \ar@{^{(}->}[r]^{f} & N \\}](/images/math/a/0/8/a084708bc461052e3d651f397327b55b.png)
The right square is a pullback, so we can use Lemma 2.3. The triangle on the left is used to compute the induced map for the identity on  , so we can use Proposition 2.2. Then we use Lemma 2.4, which shows that the map induced by the upper row is equal to the map induced by
, so we can use Proposition 2.2. Then we use Lemma 2.4, which shows that the map induced by the upper row is equal to the map induced by 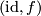 . Putting this all together we get:
. Putting this all together we get:
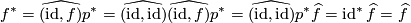

Remark 2.6.
What we saw so far implies that 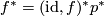 , and that for equivariant closed smooth embeddings
, and that for equivariant closed smooth embeddings 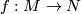 and
and 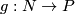 we have
we have
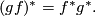
We now prove functoriality in the general case:
Proposition 2.7.
For equivariant smooth maps 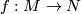 and
and 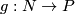 we have
we have
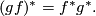
Proof. We prove the statement by showing that certain induced maps commute. For this we use the following commutative diagram
![\displaystyle \xymatrix{ & & & M\times P \ar@{->>}[dddl]^{p_P} \ar@{^{(}->}[ld]_{(id,f,id)} \\ M \ar@{^{(}->}[r]_{(id,f)} \ar@{^{(}->}[rrru]^{(id,gf)} & M\times N \ar@{^{(}->}[r]_{(id,id,g)} \ar@{->>}[d]^{p_N} & M\times N \times P \ar@{->>}[d] ^{p_{N\times P}}\\ & N \ar@{^{(}->}[r]_{(id,g)} & N\times P \ar@{->>}[d] ^{p_P}\\ & & P\\ }](/images/math/0/c/4/0c48bacf4370097077e2615f74e58caa.png)
The proof consists of three parts.
1) The middle square is a pullback, so by Lemma 2.3 we have
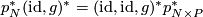 .
.
2) Lemma 2.5 for the upper triangle implies:
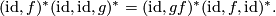
3) For the right triangle, we want to show that
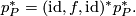
To see that, choose a of tubular neighborhood  of
of  in
in 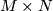 and take
and take 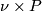 to be a tubular neighborhood of
to be a tubular neighborhood of 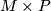 in
in 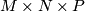 . Then the following diagram commutes
. Then the following diagram commutes
![\displaystyle \xymatrix{ M\times P \ar@{->>}[dr]^{p_P} &\nu \times P \ar@{^-->>}[l]_{(p_{\nu},\id)} \ar[r]^{(\psi,\id)} & M\times N \times P \ar@{^-->>}[dl]_{p_P} \\ & P & \\}](/images/math/4/5/6/456de551c59b9257bbcb90aca6f18b80.png)
Since all the maps here are submersions this implies what we wanted.
All this implies that:
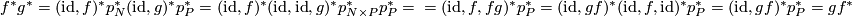

3 Extensions of cohomology theories
Often the functors map to the category of graded groups and fulfil the axioms of a cohomology theory on the category of smooth manifolds and submersions. This means that it is a homotopy functor together with a Meyer-Vietoris sequence for each equivariant open covering 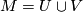 which is natural with respect to induced maps, meaning that if
which is natural with respect to induced maps, meaning that if 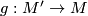 is a submersion and
is a submersion and 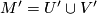 and
and 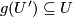 and
and 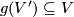 , then the corresponding diagram of Meyer-Vietoris sequences and restriction of the induces maps commutes.
, then the corresponding diagram of Meyer-Vietoris sequences and restriction of the induces maps commutes.
Lemma 3.1. In such a situation the extension of the functor to the category of smooth manifolds and smooth maps is again a cohomology theory.
Proof.
We have to show that the Mayer-Vietoris sequence is natural with respect to all equivariant smooth maps of triads. We already know that it is natural with respect to equivariant submersions of triads. Another case where naturality follows from naturality for submersions is the following. Let 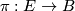 be an equivariant vector bundle, and
be an equivariant vector bundle, and 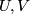 an equivariant open covering of
an equivariant open covering of  and denote by
and denote by 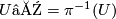 and
and 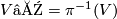 . Then the zero section
. Then the zero section 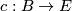 induces a map of triads (we call such a map a zero section of triads), where all induced maps are the inverses of the induced maps for the projection
induces a map of triads (we call such a map a zero section of triads), where all induced maps are the inverses of the induced maps for the projection  , hence the naturality follows from the naturality for submersions. Therefore, we will be done if we show that every equivariant smooth map of triads factors as the composition of a zero section of triads and an equivariant submersion of triads.
Since we already know that every equivariant smooth map factors as the composition of a zero section of an equivariant vector bundle and a submersion, it will be enough to show that every zero section in an equivariant vector bundle can be factored as a zero section of triads and an equivariant submersion of triads. We use the notation as above, and let
, hence the naturality follows from the naturality for submersions. Therefore, we will be done if we show that every equivariant smooth map of triads factors as the composition of a zero section of triads and an equivariant submersion of triads.
Since we already know that every equivariant smooth map factors as the composition of a zero section of an equivariant vector bundle and a submersion, it will be enough to show that every zero section in an equivariant vector bundle can be factored as a zero section of triads and an equivariant submersion of triads. We use the notation as above, and let 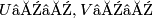 be an open cover of
be an open cover of  . There exists an invariant Riemannian metric on
. There exists an invariant Riemannian metric on  such that the intersection of
such that the intersection of 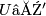 and
and 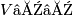 with the open unit disk bundle
with the open unit disk bundle 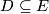 contains the intersection of
contains the intersection of 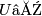 and
and 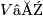 with
with 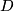 . Then the map
. Then the map 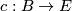 factors as a zero section of triads
factors as a zero section of triads 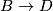 (with the open covering
(with the open covering 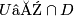 and
and 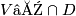 ) and the submersion (open inclusion)
) and the submersion (open inclusion) 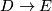 .
.

4 Applications
This extension is used in our geometric description of ordinary cohomology of Hilbert manifolds [Kreck&Tene2016].
As another application we consider the functor assigning to a finite dimensional  -manifold
-manifold  the group
the group 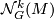 of cobordism classes of pairs
of cobordism classes of pairs 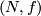 , where
, where  is a
is a  -manifold with
-manifold with 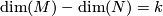 and
and 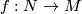 is a proper, equivariant, smooth map. This is a homotopy functor on the category of smooth
is a proper, equivariant, smooth map. This is a homotopy functor on the category of smooth  -manifolds and equivariant submersions, where induced maps are given by the pullback. Our condition is in general not fulfilled. To achieve this one passes to the cofiltered limit
-manifolds and equivariant submersions, where induced maps are given by the pullback. Our condition is in general not fulfilled. To achieve this one passes to the cofiltered limit 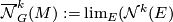 , where the limit is taken over the cofiltered category of
, where the limit is taken over the cofiltered category of  -vector bundles
-vector bundles 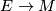 with morphisms equivariant linear submersions
with morphisms equivariant linear submersions 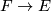 . This way we make sure that our condition is fulfilled for
. This way we make sure that our condition is fulfilled for 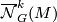 . By standard considerations one proves that this is a generalized equivariant cohomology theory. When
. By standard considerations one proves that this is a generalized equivariant cohomology theory. When  is the trivial group this theory agrees with non-oriented cobordism.
is the trivial group this theory agrees with non-oriented cobordism.
If one replaces in this example 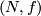 by
by 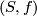 , where
, where  is a stratifold (see [Kreck2010]), one obtains another cohomology theory on the category of smooth
is a stratifold (see [Kreck2010]), one obtains another cohomology theory on the category of smooth  -manifolds and equivariant maps, denoted by
-manifolds and equivariant maps, denoted by 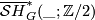 .
.
Remark 4.1.
When  is finite one can show that
is finite one can show that 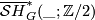 is naturally isomorphic to the cohomology of the Borel construction. We plan to study such extensions in a separate paper.
is naturally isomorphic to the cohomology of the Borel construction. We plan to study such extensions in a separate paper.
5 References
- [Hirsch1976] M. W. Hirsch, Differential topology., Graduate Texts in Mathematics, No. 33. Springer-Verlag., New York-Heidelberg, 1976. MR0448362 (56 #6669) Zbl 0356.57001
- [Kreck&Tene2016] M. Kreck and H. Tene, Hilbert stratifolds and a Quillen type geometric description of cohomology for Hilbert manifolds, (2016). Available at the arXiv:1506.07075v2
- [Kreck2010] M. Kreck, Differential algebraic topology, Graduate Studies in Mathematics, 110, American Mathematical Society, 2010. MR2641092 (2011i:55001) Zbl 05714474
- [Lang1999] S. Lang, Fundamentals of differential geometry, Graduate Texts in Mathematics, 191. Springer-Verlag, New York, 1999. MR1666820 Zbl 0932.53001