Curvature identities
|
The user responsible for this page is Jost Eschenburg. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
Let  be a smooth manifold and
be a smooth manifold and  a vector bundle over
a vector bundle over  with
covariant derivative
with
covariant derivative  . Let
. Let ![R_{ij} = R(\phi_i,\phi_j) = [\nabla_i,\nabla_j]](/images/math/5/1/f/51fcc2c5b9fd669b746738afa29634bc.png) be the curvature tensor with respect to a local parametrization
be the curvature tensor with respect to a local parametrization
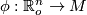 where
where 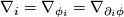 .
By definition,
.
By definition,
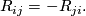
If  carries an inner product
carries an inner product 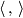 on each of its fibres and if
on each of its fibres and if  is metric, i.e. for any two section
is metric, i.e. for any two section
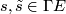 the inner product satisfies the product rule
the inner product satisfies the product rule
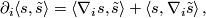
then the expression 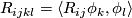 is skew symmetric also in
the last two indices:
is skew symmetric also in
the last two indices:
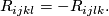
Now suppose that on the tangent bundle  there is another covariant derivative
there is another covariant derivative
 which is torsion free,
which is torsion free, 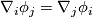 . Then
the tensor derivative
. Then
the tensor derivative 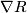 of
of  is defined:
is defined:
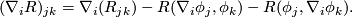
Abbreviating 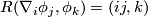 (symmetric in the first two indices
(symmetric in the first two indices  and
and  ),
we have
),
we have 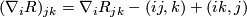 , using the antisymmetry (1)
and the torsion freeness. Now the cyclic sum of the last two
, using the antisymmetry (1)
and the torsion freeness. Now the cyclic sum of the last two
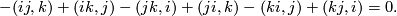
Tex syntax erroris
![\displaystyle \nabla_i(R_{jk}) = [\nabla_i,R_{jk}] = [\nabla_i,[\nabla_j,\nabla_k]].](/images/math/e/4/d/e4dc3588187f55f39b0008677a43af2c.png)
Thus we obtain an identity for 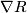 , sometimes called the Second Bianchi Identity
, sometimes called the Second Bianchi Identity
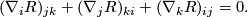
When  is a torsion free covariant derivative on the tangent bundle
is a torsion free covariant derivative on the tangent bundle  , there is
in addition the First Bianchi Identity: Putting
, there is
in addition the First Bianchi Identity: Putting 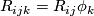 , we have
, we have
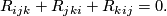
In fact,
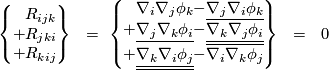
An algebraic consequence is the block symmetry:
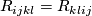
In fact, putting 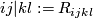 and applying (4), (1), (2) we obtain
(expressions with equal parentheses cancel each other):
and applying (4), (1), (2) we obtain
(expressions with equal parentheses cancel each other):
![\displaystyle 0 = \left\{\begin{matrix} \ \ \,{ij|kl} \cr +\, (jk|il) \cr +\, [ki|jl] \end{matrix}\right\} + \left\{\begin{matrix} \ \ \,{ji|lk} \cr +\, \langle il|jk\rangle \cr + \{lj|ik\} \end{matrix} \right\}- \left\{\begin{matrix} \ \ \,{kl|ij} \cr +\, \langle li|kj\rangle \cr +\, [ik|lj] \end{matrix} \right\}- \left\{\begin{matrix} \ \ \,{lk|ji} \cr +\, (kj|li) \cr + \{jl|ki\} \end{matrix}\right\} = 2(ij|kl - kl|ij)](/images/math/5/0/d/50dee8473db55d9d4ff555a718436203.png)
Equations (1), (2), (4), (5) are the algebraic identities for the
curvature tensor of the Levi-Civita derivative, the Riemannian curvature tensor.
By (1), (2), (5), a Riemannian curvature tensor
can be viewed as a section of 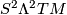 , a symmetric bilinear form on
, a symmetric bilinear form on 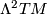 .
The antisymmetric 4-forms form another subspace
.
The antisymmetric 4-forms form another subspace 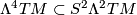 , and the
additional identity (4) characterizes precisely
the orthogonal complement of
, and the
additional identity (4) characterizes precisely
the orthogonal complement of 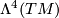 in
in 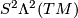 .
.