Cell attachments for surgery (Ex)

The exercises on this page come directly from [Lück2001, pp. 70-71] and we use the notation found there.

Let 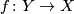$f \colon Y \to X$$\newcommand{\Z}{\mathbb{Z}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\N}{\mathbb{N}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\F}{\mathbb{F}} \newcommand{\bZ}{\mathbb{Z}} \newcommand{\bR}{\mathbb{R}} \newcommand{\bC}{\mathbb{C}} \newcommand{\bH}{\mathbb{H}} \newcommand{\bQ}{\mathbb{Q}} \newcommand{\bF}{\mathbb{F}} \newcommand{\bN}{\mathbb{N}} \DeclareMathOperator\id{id} % identity map \DeclareMathOperator\Sq{Sq} % Steenrod squares \DeclareMathOperator\Homeo{Homeo} % group of homeomorphisms of a topoloical space \DeclareMathOperator\Diff{Diff} % group of diffeomorphisms of a smooth manifold \DeclareMathOperator\SDiff{SDiff} % diffeomorphism under some constraint \DeclareMathOperator\Hom{Hom} % homomrphism group \DeclareMathOperator\End{End} % endomorphism group \DeclareMathOperator\Aut{Aut} % automorphism group \DeclareMathOperator\Inn{Inn} % inner automorphisms \DeclareMathOperator\Out{Out} % outer automorphism group \DeclareMathOperator\vol{vol} % volume \newcommand{\GL}{\text{GL}} % general linear group \newcommand{\SL}{\text{SL}} % special linear group \newcommand{\SO}{\text{SO}} % special orthogonal group \newcommand{\O}{\text{O}} % orthogonal group \newcommand{\SU}{\text{SU}} % special unitary group \newcommand{\Spin}{\text{Spin}} % Spin group \newcommand{\RP}{\Rr\mathrm P} % real projective space \newcommand{\CP}{\Cc\mathrm P} % complex projective space \newcommand{\HP}{\Hh\mathrm P} % quaternionic projective space \newcommand{\Top}{\mathrm{Top}} % topological category \newcommand{\PL}{\mathrm{PL}} % piecewise linear category \newcommand{\Cat}{\mathrm{Cat}} % any category \newcommand{\KS}{\text{KS}} % Kirby-Siebenmann class \newcommand{\Hud}{\text{Hud}} % Hudson torus \newcommand{\Ker}{\text{Ker}} % Kernel \newcommand{\underbar}{\underline} %Classifying Spaces for Families of Subgroups \newcommand{\textup}{\text} \newcommand{\sp}{^}f \colon Y \to X$ be a map of CW-complexes and let 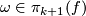$\omega \in \pi_{k+1}(f)$$\omega \in \pi_{k+1}(f)$ be represented by the following commutative diagram

$\displaystyle \xymatrix{S^k \ar[r]^q \ar[d]_j & Y \ar[d]^f \\ D^{k+1} \ar[r]^{Q} & X}.$

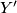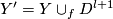Let $Y'$$Y'$ be the push out of $q$$q$: i.e. $Y'=Y \cup_f D^{l+1}$$Y'=Y \cup_f D^{l+1}$ is the space obtained by attaching an 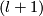$(l+1)$$(l+1)$-cell to $Y$$Y$ along $f$$f$. There is an induced map

$\displaystyle f' \colon Y' \to X.$ $$\displaystyle f' \colon Y' \to X.$$

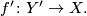
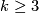Exercise 0.1. With notation above assume that $f$$f$ is $k$$k$-connected with $k \geq 3$$k \geq 3$. Prove that the kernel of the surjection 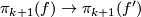$\pi_{k+1}(f) \to \pi_{k+1}(f')$$\pi_{k+1}(f) \to \pi_{k+1}(f')$ is the 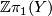$\Zz \pi_1(Y)$$\Zz \pi_1(Y)$-module generated by $\omega$$\omega$.

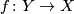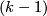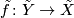Exercise 0.2 [Lück2001, Lemma 3.55]. Let $f \colon Y \to X$$f \colon Y \to X$ be a $(k-1)$$(k-1)$-connected map of CW-complexes for some $k \geq 2$$k \geq 2$ where $X$$X$ is connected. Consider a lift $\tilde f \colon \tilde Y \to \tilde X$$\tilde f \colon \tilde Y \to \tilde X$ on the universal coverings. Show the following:

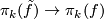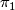1. The natural map $\pi_k(\tilde f) \to \pi_k(f)$$\pi_k(\tilde f) \to \pi_k(f)$ is $\pi_1$$\pi_1$-equivariant and bijective.
2. The homology groups 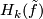$H_k(\tilde f)$$H_k(\tilde f)$ are finitely generated 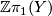$\Zz\pi_1(Y)$$\Zz\pi_1(Y)$ modules.
3. One can make $f$$f$ $k$$k$-connected by attaching finitely many cells.

The exercises on this page were sent by Nicolas Ginoux and Carolina Neira-Jiménez.