Blanchfield form
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Background: equivariant intersection forms
In 1939 Reidemeister [Reidemeister1939] defined an equivariant, sesquilinear intersection form on the homology of a covering space  of an
of an  -dimensional closed manifold
-dimensional closed manifold  whose deck transformation group
whose deck transformation group  is abelian.
is abelian.
![\displaystyle \begin{array}{rcl} I_{\widetilde{M}} \colon H_k(\widetilde{M};\mathbb{Z}) \times H_{m-k}(\widetilde{M};\mathbb{Z}) &\to & \mathbb{Z}[G]; \\ ([p],[q]) & \mapsto & \sum_{g \in G} \langle g \cdot p, q \rangle g^{-1}, \end{array}](/images/math/9/5/f/95ff1aef5a0aeceaa0a316f97a96c1d3.png)
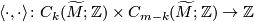
The intersections of each possible  -translate of
-translate of  and
and  are counted, and indexed according to the deck transformation which produced that intersection number.
are counted, and indexed according to the deck transformation which produced that intersection number.
[edit] 2 Definition of the Blanchfield form
In his 1954 Princeton PhD thesis R. C. Blanchfield [Blanchfield1957] made the corresponding generalisation for linking forms. Let 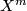 be a compact manifold, now possibly with non-empty boundary, with a surjective homomorphism
be a compact manifold, now possibly with non-empty boundary, with a surjective homomorphism 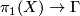 , for some free abelian group
, for some free abelian group 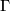 . Let
. Let ![\mathbb{Z}[\Gamma]](/images/math/a/3/1/a3125186741639dcc06e77c618736635.png) be the group ring of
be the group ring of 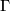 and let
and let 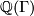 be its field of fractions.
be its field of fractions.
![\mathbb{Z}[\Gamma]](/images/math/a/3/1/a3125186741639dcc06e77c618736635.png) -torsion submodule of a
-torsion submodule of a ![\mathbb{Z}[\Gamma]](/images/math/a/3/1/a3125186741639dcc06e77c618736635.png) module
module  is the submodule
is the submodule ![\displaystyle TP:= \{p \in P \,|\, ap=0 \text{ for some } a \in \mathbb{Z}[\Gamma]\}.](/images/math/2/3/6/236be0676d35583ae0d92faf468aa3cc.png)
The Blanchfield form is a sesquilinear ![\mathbb{Q}(\Gamma)/\mathbb{Z}[\Gamma]](/images/math/b/0/5/b053dfff634dbdd57961d4231aab4d20.png) --valued pairing which is defined on the
--valued pairing which is defined on the ![\mathbb{Z}[\Gamma]](/images/math/a/3/1/a3125186741639dcc06e77c618736635.png) -torsion submodules of the homology of the
-torsion submodules of the homology of the 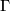 --cover
--cover  of
of  :
:
![\displaystyle \mathop{\mathrm{Bl}} \colon TH_\ell(\widetilde{X};\mathbb{Z}) \times TH_{m-\ell-1}(\widetilde{X},\partial\widetilde{X};\mathbb{Z}) \to \mathbb{Q}(\Gamma)/\mathbb{Z}[\Gamma].](/images/math/6/8/e/68e7badc994282925b3d2464324f747e.png)
![\displaystyle [x] \in TH_\ell(\widetilde{X};\mathbb{Z}) \cong TH_\ell(X;\mathbb{Z}[\Gamma])](/images/math/d/5/5/d55dd349382e40c3e000068222d15ffe.png)
![\displaystyle [y] \in TH_{m-\ell-1}(\widetilde{X},\partial \widetilde{X};\mathbb{Z}) \cong TH_{m-\ell-1}(X,\partial X;\mathbb{Z}[\Gamma])](/images/math/a/1/2/a1287db438b45a10e05cb69d69c33415.png)
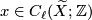 and
and 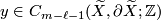 , let
, let 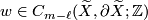 be such that
be such that 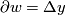 , for some
, for some ![\Delta \in \mathbb{Z}[\Gamma]](/images/math/0/3/a/03a07519b417c559188d4f50e3899ac2.png) . Then we define:
. Then we define:
![\displaystyle \mathop{\mathrm{Bl}}([x],[y]) := \sum_{g \in \Gamma} \langle g \cdot x, w \rangle g^{-1}/\Delta \in \mathbb{Q}(\Gamma)/\mathbb{Z}[\Gamma],](/images/math/a/f/3/af39d01e2093f30d56fb279124d600f7.png)
where 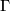 acts on
acts on 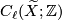 by the action induced from the deck transformation.
by the action induced from the deck transformation.
The Blanchfield form can also be defined via homology, using a Bockstein homomorphism and a cup product. This is entirely analogous to the treatment the situation with the linking form. Just change  to
to ![\mathbb{Z}[\mathbb{Z}]](/images/math/1/4/5/145a993dc91cbaa4548057383bb478b1.png) and
and 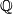 to
to 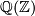 . In the case of knot exteriors, a homological definition is also given below.
. In the case of knot exteriors, a homological definition is also given below.
[edit] 3 Example of knot exteriors
We now turn to an example. We will focus on the case of knots in  . For a knot
. For a knot 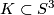 , let
, let 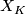 denote its exterior, which is the complement of a regular neighbourhood of
denote its exterior, which is the complement of a regular neighbourhood of  :
: 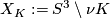 . Now
. Now 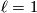 ,
, 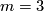 and the abelianisation gives a homomorphism
and the abelianisation gives a homomorphism 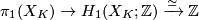 . The Blanchfield form can in this case be defined without relative homology, on
. The Blanchfield form can in this case be defined without relative homology, on ![H_1(X_K;\mathbb{Z}[\mathbb{Z}]) \cong H_1(\widetilde{X}_K;\mathbb{Z})](/images/math/3/0/a/30a5f3c1b63fd8fb88f048752cb3b0ed.png) . The form
. The form
![\displaystyle \mathop{\mathrm{Bl}} \colon H_1(X_K;\mathbb{Z}[\mathbb{Z}]) \times H_1(X_K;\mathbb{Z}[\mathbb{Z}]) \to \mathbb{Q}(\mathbb{Z})/\mathbb{Z}[\mathbb{Z}]](/images/math/8/3/b/83bf910881a456853f02bd9e86db3391.png)
is non--singular, sesquilinear and Hermitian. Note that ![H_1(X_K;\mathbb{Z}[\mathbb{Z}])](/images/math/4/6/b/46b729298a9b112e3dec6fe78d83b20c.png) is entirely
is entirely ![\mathbb{Z}[\mathbb{Z}]](/images/math/1/4/5/145a993dc91cbaa4548057383bb478b1.png) -torsion, so
-torsion, so ![H_1(X_K;\mathbb{Z}[\mathbb{Z}]) = TH_1(X_K;\mathbb{Z}[\mathbb{Z}])](/images/math/d/8/9/d89fcb6c4897f5d3d28aed868a29c8ea.png) . The adjoint of this form is given by the following sequence of homomorphisms:
. The adjoint of this form is given by the following sequence of homomorphisms:
![\displaystyle \begin{aligned} &H_1(X_K;\mathbb{Z}[\mathbb{Z}]) \to H_1(X_K,\partial X_K;\mathbb{Z}[\mathbb{Z}]) \to H^2(X_K;\mathbb{Z}[\mathbb{Z}]) \\ & \to H^1(X_K;\mathbb{Q}(\mathbb{Z})/\mathbb{Q}[\mathbb{Z}]) \to \Hom_{\mathbb{Z}[\mathbb{Z}]}(H_1(X_K;\mathbb{Z}[\mathbb{Z}]),\mathbb{Q}(\mathbb{Z})/\mathbb{Q}[\mathbb{Z}]), \end{aligned}](/images/math/c/5/f/c5f646cf3978122201f5ffd09c06f0d7.png)
which arise from the long exact sequence of a pair, equivariant Poincaré-Lefschetz duality, a Bockstein homomorphism, and universal coefficients. Showing that these maps are isomorphisms proves that 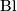 is non-singular. A good exercise is to trace through this sequence of isomorphisms to check that it really does coincide with the definition of the Blanchfield form given above.
is non-singular. A good exercise is to trace through this sequence of isomorphisms to check that it really does coincide with the definition of the Blanchfield form given above.
A formula for the Blanchfield pairing of a knot in terms of a Seifert matrix for it is given in [Kearton1975]. The algebraic relationship between Seifert matrices and the Blanchfield pairing was studied in [Trotter1973],[Trotter1978] and [Ranicki2003]. In particular, every Blanchfield form is determined by a Seifert matrix, and two Seifert matrices are  -equivalent (resp. cobordant) if and only if they determine isomorphic (resp. cobordant) Blanchfield forms.
-equivalent (resp. cobordant) if and only if they determine isomorphic (resp. cobordant) Blanchfield forms.
[edit] 4 Applications to knot concordance
 are concordant if there is an annulus embedded in
are concordant if there is an annulus embedded in  whose boundary is
whose boundary is 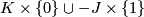 . A knot which is concordant to the unknot is called a slice knot; equivalently a slice knot bounds an embedded disk in
. A knot which is concordant to the unknot is called a slice knot; equivalently a slice knot bounds an embedded disk in 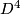 . We say that a Blanchfield form is metabolic if there is a submodule
. We say that a Blanchfield form is metabolic if there is a submodule ![P \subset H_1(X_K;\mathbb{Z}[\mathbb{Z}])](/images/math/9/3/8/938003a52a52d5c1016d2ad7d6deaa60.png) which is self-orthogonal with respect to
which is self-orthogonal with respect to 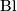 , called a metaboliser. The Blanchfield form of a slice knot is metabolic, so that the Blanchfield form provides an obstruction to concordance [Kearton1975], which is equivalent to Levine's Seifert form obstruction [Levine1969a], but which is more intrinsic, since for a given knot there are potentially many Seifert surfaces but only one knot exterior. The proof that the Blanchfield form of a slice knot is metabolic rests on the observation that, if
, called a metaboliser. The Blanchfield form of a slice knot is metabolic, so that the Blanchfield form provides an obstruction to concordance [Kearton1975], which is equivalent to Levine's Seifert form obstruction [Levine1969a], but which is more intrinsic, since for a given knot there are potentially many Seifert surfaces but only one knot exterior. The proof that the Blanchfield form of a slice knot is metabolic rests on the observation that, if 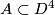 is a slice disk for
is a slice disk for  , the Blanchfield form vanishes on the kernel of the inclusion induced map
, the Blanchfield form vanishes on the kernel of the inclusion induced map ![\displaystyle H_1(X_K;\mathbb{Z}[\mathbb{Z}]) \to H_1(D^4\setminus \nu A;\mathbb{Z}[\mathbb{Z}]).](/images/math/6/0/b/60b126ae6a3f36837e2e3b54015454e9.png)
For high-dimensional knots, 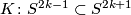 , where
, where 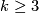 , the Blanchfield form is metabolic if and only if
, the Blanchfield form is metabolic if and only if  is slice [Levine1969a], [Kearton1975]. Levine [Levine1977] classified the modules which can arise as the homology of high-dimensional knots: the key property that a knot module must satisfy is Blanchfield duality. For a comprehensive account of the algebraic theory of high-dimensional knots, such as how the Blanchfield form can be used to compute the high-dimensional knot cobordism group, see [Ranicki1998].
is slice [Levine1969a], [Kearton1975]. Levine [Levine1977] classified the modules which can arise as the homology of high-dimensional knots: the key property that a knot module must satisfy is Blanchfield duality. For a comprehensive account of the algebraic theory of high-dimensional knots, such as how the Blanchfield form can be used to compute the high-dimensional knot cobordism group, see [Ranicki1998].
For classical knots in the  -sphere, there are many non-slice knots with metabolic Blanchfield form, the first of which were found in [Casson&Gordon1986]. Cochran, Orr and Teichner [Cochran&Orr&Teichner2003] defined an infinite filtration of the knot concordance group, each of whose associated graded groups has infinite rank [Cochran&Orr&Teichner2004], [Cochran&Teichner2007], [Cochran&Harvey&Leidy2009]. Their obstructions are obtained by defining representations into progressively more solvable groups. The Blanchfield form, and so-called higher order Blanchfield forms, play a crucial role in controlling the representations which extend from the knot exterior across a potential slice disc exterior
-sphere, there are many non-slice knots with metabolic Blanchfield form, the first of which were found in [Casson&Gordon1986]. Cochran, Orr and Teichner [Cochran&Orr&Teichner2003] defined an infinite filtration of the knot concordance group, each of whose associated graded groups has infinite rank [Cochran&Orr&Teichner2004], [Cochran&Teichner2007], [Cochran&Harvey&Leidy2009]. Their obstructions are obtained by defining representations into progressively more solvable groups. The Blanchfield form, and so-called higher order Blanchfield forms, play a crucial role in controlling the representations which extend from the knot exterior across a potential slice disc exterior  , whose existence one wishes to deny. Let
, whose existence one wishes to deny. Let 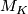 be the closed 3-manifold obtained from zero-framed surgery on
be the closed 3-manifold obtained from zero-framed surgery on  along
along  . Note that
. Note that 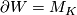 . Then the kernel
. Then the kernel
![\displaystyle P:= \ker(H_1(M_K;\mathbb{Q}[\mathbb{Z}]) \to H_1(W;\mathbb{Q}[\mathbb{Z}]))](/images/math/0/2/c/02ccdfcc84890179b9f6e1a8562afd3d.png)
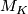 . Therefore, given
. Therefore, given 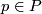 , the representation
, the representation ![\displaystyle H_1(M_K;\mathbb{Q}[\mathbb{Z}]) \to \mathbb{Q}(\mathbb{Z})/\mathbb{Q}[\mathbb{Z}];\; x \mapsto \mathop{\mathrm{Bl}}(p,x)](/images/math/e/d/a/eda3ac9ad1e52f718ad1762a9101c66b.png)
extends over  .
.
We give a special case of the results of [Cochran&Orr&Teichner2003] below, which shows the use of the Blanchfield form in an archetypal obstruction theorem for knot concordance problems. Given a closed 3-manifold  and a representation
and a representation 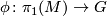 there is defined a real number
there is defined a real number 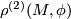 called the Cheeger-Gromov-Von Neumann
called the Cheeger-Gromov-Von Neumann  -invariant of
-invariant of 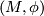 , which can be computed using
, which can be computed using 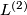 -signatures of 4-manifolds with boundary
-signatures of 4-manifolds with boundary 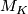 .
.
Theorem 4.1 (Cochran-Orr-Teichner).
Let  be a slice knot. Then there exists a metaboliser
be a slice knot. Then there exists a metaboliser 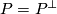 for the rational Blanchfield form of
for the rational Blanchfield form of  such that for each
such that for each 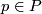 there is a representation
there is a representation 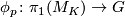 for which
for which 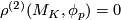 .
.
Finally, it is somewhat remarkable that the classical Blanchfield form continues to have new and interesting applications. For example, Borodzik and Friedl [Borodzik&Friedl2012] recently used the minimal size of a square matrix which presents the Blanchfield form of a given knot to compute many previously unknown unknotting numbers of low crossing number knots. See the linking form page, for the definition of a presentation of a linking form.
[edit] 5 References
- [Blanchfield1957] R. C. Blanchfield, Intersection theory of manifolds with operators with applications to knot theory, Ann. of Math. (2) 65 (1957), 340–356. MR0085512 (19,53a) Zbl 0080.16601
- [Borodzik&Friedl2012] M. Borodzik and S. Friedl, The unknotting number and classical invariants I, (2012). Available at the arXiv:1203.3225.
- [Casson&Gordon1986] A. J. Casson and C. M. Gordon, Cobordism of classical knots, with an appendix by P. M. Gilmer. Progr. Math., 62, À la recherche de la topologie perdue, 181–199, Birkhäuser Boston, Boston, MA, 1986. MR900252
- [Cochran&Harvey&Leidy2009] T. D. Cochran, S. Harvey and C. Leidy, Knot concordance and higher-order Blanchfield duality, Geom. Topol. 13 (2009), no.3, 1419–1482. MR2496049 (2009m:57006) Zbl 1175.57004
- [Cochran&Orr&Teichner2003] T. D. Cochran, K. E. Orr and P. Teichner, Knot concordance, Whitney towers and
 -signatures, Ann. of Math. (2) 157 (2003), no.2, 433–519. MR1973052 (2004i:57003) Zbl 1044.57001
-signatures, Ann. of Math. (2) 157 (2003), no.2, 433–519. MR1973052 (2004i:57003) Zbl 1044.57001
- [Cochran&Orr&Teichner2004] T. D. Cochran, K. E. Orr and P. Teichner, Structure in the classical knot concordance group, Comment. Math. Helv. 79 (2004), no.1, 105–123. MR2031301 (2004k:57005) Zbl 1061.57008
- [Cochran&Teichner2007] T. D. Cochran and P. Teichner, Knot concordance and von Neumann
 -invariants, Duke Math. J. 137 (2007), no.2, 337–379. MR2309149 (2008f:57005) Zbl 1186.57006
-invariants, Duke Math. J. 137 (2007), no.2, 337–379. MR2309149 (2008f:57005) Zbl 1186.57006
- [Fox&Milnor1966] R. H. Fox and J. W. Milnor, Singularities of
 -spheres in
-spheres in  -space and cobordism of knots, Osaka J. Math. 3 (1966), 257–267. MR0211392 (35 #2273) Zbl 0146.45501
-space and cobordism of knots, Osaka J. Math. 3 (1966), 257–267. MR0211392 (35 #2273) Zbl 0146.45501
- [Kearton1975] C. Kearton, Cobordism of knots and Blanchfield duality, J. London Math. Soc. (2) 10 (1975), no.4, 406–408. MR0385873 (52 #6732) Zbl 0305.57015
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Levine1977] J. Levine, Knot modules. I, Trans. Amer. Math. Soc. 229 (1977), 1–50. MR0461518 (57 #1503) Zbl 0422.57007
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Ranicki2003] A. Ranicki, Blanchfield and Seifert algebra in high-dimensional knot theory, Mosc. Math. J. 3 (2003), no.4, 1333–1367. MR2058802 (2005b:19008) Zbl 1059.19003
- [Reidemeister1939] K. Reidemeister, Durchschnitt und Schnitt von Homotopieketten, Monatsh. Math. Phys. 48 (1939), 226–239. MR0000634 (1,105h) Zbl 0021.43104
- [Trotter1973] H. F. Trotter, On
 -equivalence of Seifert matrices, Invent. Math. 20 (1973), 173–207. MR0645546 (58 #31100) Zbl 0269.15009
-equivalence of Seifert matrices, Invent. Math. 20 (1973), 173–207. MR0645546 (58 #31100) Zbl 0269.15009
- [Trotter1978] H. F. Trotter, Knot module and Seifert matrices, Knot theory (Proc. Sem., Plans-sur-Bex, 1977), Springer (1978), 291–299. MR521739 (81c:57019) Zbl 407.57015