Axiomatization of the manifold concept
|
This page has not been refereed. The information given here might be incomplete or provisional. |
[edit] 1 Background (ca. 1854 to 1930)
For B. Riemann it was an intricate task to formulate his general concept of manifolds (discrete or continuous) in 1854. At that time, it was technically impossible to give a formal definition of topological spaces and to specify manifolds among them. Not even a general concept of set was around; Riemann's step rather contributed to bring it about [Ferreiros1999]. Around the turn from the 19th to the 20th century the situation started to change [Scholz1999]:
- In his series on analysis situs (1895ff. [Poincaré2010]) H. Poincaré gave two general constructive definitions and some special construction procedures for manifolds; as building material he still used subsets of
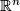 [Sarkaria1999].
[Sarkaria1999].
- D. Hilbert indicated how to characterize the topological properties of the Euclidean plane in an appendix to his foundations of geometry (1902f.); H. Weyl took the idea up in his book on the Riemann surfaces (1913).
- Point sets had been considered by G. Cantor since his first works on transfinite set theory, and attracted attention by W.H. and G.C. Young (1906), A. Schoenflies (1900, 1908) and others. In his studies of generalized limits M.Fréchet (1906) and F.Riesz, in an attempt to found a general notion of space (1907), introduced the first axiomatizations of topological spaces [Rodriguez2006].
- Finally a general axiomatic concept of topological space (including separation properties) was introduced by F. Hausdorff in Grundzüge der Mengenlehre ([Hausdorff1914]).
Poincaré's constructive approach inspired his successors to try a route toward a combinatorial definition of manifolds ([Dehn&Heegaard1907], [Tietze1908]). A crucial stumbling block for this approach lay in the necessity to assume the existence of a common subdivision for two cell decompositions of a manifold given by other means (e.g. as a singularity free subvariety of 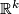 or
or 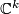 ), a little later called the Hauptvermutung by H. Kneser. A purely combinatorial approach would, moreover, presuppose an appropriate equivalence concept for combinatorially defined spaces, which was difficult to find. L.E.J. Brouwer developed independently the ideas of a piecewise linear representation of manifolds and of mapping degree. The strength of his method became clear in his proofs of the invariance of dimension ([Brouwer1911], [Brouwer1911a]).
), a little later called the Hauptvermutung by H. Kneser. A purely combinatorial approach would, moreover, presuppose an appropriate equivalence concept for combinatorially defined spaces, which was difficult to find. L.E.J. Brouwer developed independently the ideas of a piecewise linear representation of manifolds and of mapping degree. The strength of his method became clear in his proofs of the invariance of dimension ([Brouwer1911], [Brouwer1911a]).
In spite of the difficulties mentioned, H. Weyl favoured such an approach in the 1920s because it suited his constructivist leanings in the foundations of mathematics [Weyl1924]. He was not the only one. H. Kneser, L. Vietoris and E. van Kampen proposed different versions of constructive definitions of manifolds in the spirit of Brouwer and/or Weyl ([Vietoris1926], [Vietoris1928], [van Kampen1929]).
Kneser did not exclusively rely on the constructive approach. In [Kneser1926] he discussed both, an axiomatic approach based on Hausdorff's set theoretic approach to topology, and a combinatorial one similar to Weyl's. He tried to explore the connection between the two as far as possible. For the axiomatic characterization of manifolds he limited himself to the topological case, without a discussion of differentiable structures. Kneser characterized a topological manifold  by Hausdorff's axioms for a neighbourhood basis (of a Hausdorff space) including the second countability axiom for a neighbourhood base. He added only one postulate: Each point
by Hausdorff's axioms for a neighbourhood basis (of a Hausdorff space) including the second countability axiom for a neighbourhood base. He added only one postulate: Each point 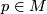 has a neighbourhood which is topologically equivalent to an open ball in the ``
has a neighbourhood which is topologically equivalent to an open ball in the `` -dimensional number space,
-dimensional number space, 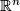 . A ``closed (in our terminology compact) manifold was characterized by the Heine-Borel criterion for open coverings of
. A ``closed (in our terminology compact) manifold was characterized by the Heine-Borel criterion for open coverings of  . Kneser's attempt to derive a combinatorial theory for an axiomatically defined compact manifold ran upon several difficulties. One was the open status of the Hauptvermutung; another one was an internal limitation of his combinatorial approach which did not allow to derive Poincaré duality for orientable manifolds by his means.
. Kneser's attempt to derive a combinatorial theory for an axiomatically defined compact manifold ran upon several difficulties. One was the open status of the Hauptvermutung; another one was an internal limitation of his combinatorial approach which did not allow to derive Poincaré duality for orientable manifolds by his means.
In a survey presented in September 1929 to the Deutsche Mathematiker-Vereinigung, B.L. van der Waerden discussed no less than five different possibilities to define topological manifolds, following different methodological approaches, one set theoretic following Kneser, two purely combinatorial ones, and two which he considered as ``mixed`` ([van der Waerden1930]).
[edit] 2 Veblen/Whitehead's axiomatics
At the turn to the 1930s the time seemed ripe for a precise formulation of the mathematical concept of manifold. The tools for clearly stating a topological definition of manifolds and for distinguishing different levels of differentiability had been prepared since the beginning of the century. O. Veblen and J.H.C. Whitehead were the ones to use them.
Already at the beginning of his mathematical career, Veblen had contributed to the foundations of geometry in the sense of Hilbert's axiomatic approach. After 1918 he turned with enthusiasm to the study of analysis situs, differential geometry, general relativity and unified field theories. In the 1920s he assembled a group of geometers around him, interested in differential geometry and analysis situs (T. Thomas, L.P. Eisenhart, later S. Lefschetz, J.H.C. Whitehead and others). Moreover, he cultivated the exchange with H. Weyl on the foundations of differential geometry. At the turn to the 1930s he and his student J.H.C. Whitehead, who had arrived from Oxford in summer 1929, attacked the problem of an axiomatic definition of manifolds with different degrees of differentiability, which lived up to the present standards of the axiomatics. A short version appeared in the Proceedings of the National Academy of Sciences [Veblen&Whitehead1931] a more extended exposition was given in their volume in the Cambridge Tracts in Mathematics and Physics [Veblen&Whitehead1932].
Unlike Kneser, Veblen and Whitehead did not presuppose the topological structure on the set which ought to become their manifold. They rather followed the spirit of a ``localized`` Kleinian concept of geometry and introduced the manifold structure by postulating a pseudogroup
which ought to become their manifold. They rather followed the spirit of a ``localized`` Kleinian concept of geometry and introduced the manifold structure by postulating a pseudogroup  of transformations of open sets (``regions``) in
of transformations of open sets (``regions``) in 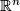 or
or 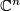 . The concept of pseudogroup had been introduced by E. Cartan in his study of local Lie groups and the question in how far a local group could be extended to a (global) Lie group [Cartan1904]. Veblen and Whitehead characterized a ``pseudogroup``
. The concept of pseudogroup had been introduced by E. Cartan in his study of local Lie groups and the question in how far a local group could be extended to a (global) Lie group [Cartan1904]. Veblen and Whitehead characterized a ``pseudogroup``  by the two postulates of conditional composition (``if the resultant of two transformations in the set exists it is also in the set``) and of the existence of inverses [Veblen&Whitehead1932]. The possibility to restrict a transformation
by the two postulates of conditional composition (``if the resultant of two transformations in the set exists it is also in the set``) and of the existence of inverses [Veblen&Whitehead1932]. The possibility to restrict a transformation 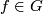 ,
, 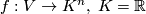 or
or Tex syntax error, to
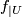 for
for  was not explicitly stated as axiom of their ``pseudogroups; but it was indirectly implied by their conditions on allowable coordinate systems ((A3), see below).[1] Their pseudogroup defined a class u of transformations. Their main examples were what today would be called
was not explicitly stated as axiom of their ``pseudogroups; but it was indirectly implied by their conditions on allowable coordinate systems ((A3), see below).[1] Their pseudogroup defined a class u of transformations. Their main examples were what today would be called 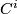 -transformations of open sets in
-transformations of open sets in 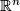 (
(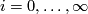 ), or analytic, locally invertible funcitons in
), or analytic, locally invertible funcitons in 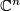 ; but their ``class
; but their ``class  `` could also be chosen to designate other structures characterized by affine linear, or volume preserving transformations, etc.
`` could also be chosen to designate other structures characterized by affine linear, or volume preserving transformations, etc.
To define an  -dimensional manifold of class u, Veblen and Whitehead considered the pseudogroup of transformations of ``class
-dimensional manifold of class u, Veblen and Whitehead considered the pseudogroup of transformations of ``class  ``. The structure of an
``. The structure of an  -dimensional manifold of class
-dimensional manifold of class  in their sense was specified by a system of allowable coordinate systems
in their sense was specified by a system of allowable coordinate systems 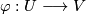 with bijective maps
with bijective maps 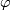 onto regions
onto regions 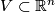 , defined for a sufficiently large collection of ``domains``
, defined for a sufficiently large collection of ``domains`` 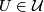 ,
, 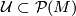 , such that three groups of axioms hold:
, such that three groups of axioms hold:
I. Basic axioms for admissible coordinate systems:
- [(A1)] For two allowable coordinate systems with the same domain,
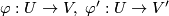 , the corresponding coordinate transformation
, the corresponding coordinate transformation 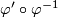 belongs to the pseudogroup of class u (is
belongs to the pseudogroup of class u (is  -regular), if
-regular), if  or
or 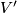 is a region.
is a region.
- [(A2)] A
 -regular transformation (
-regular transformation (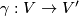 ) concatenated with an allowable coordinate system (
) concatenated with an allowable coordinate system (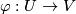 ) leads to an allowable coordinate system (
) leads to an allowable coordinate system (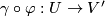 ).
).
- [(A3)] Restriction of an allowable coordinate system to the counter-image of a ball in number space is an allowable coordinate system.
The counter-image of a ball in number space was called, in general, an n-cell by Veblen and Whitehead.
II. Union of compatible coordinate systems
- [(B1)] The union of admissible coordinate systems, compatible on overlaps and with
 -cells as domains, is an admissible coordinate system.
-cells as domains, is an admissible coordinate system.
- [(B2)] On the other hand, each allowable coordinate system can be gained as a union of admissible coordinate systems with
 -cells as domains.
-cells as domains.
III. Topological axioms, in particular separability
- [(C1)] If two
 -cells (
-cells ( and
and 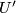 ) have a point
) have a point  in common, they have an
in common, they have an  -cell in common (
-cell in common (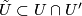 ) which contains this point (
) which contains this point (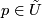 ).
).
- [(C2)] To any two distinct points
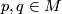 there exist disjoint
there exist disjoint  -cells
-cells 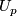 and
and 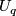 which contain respectively
which contain respectively  or
or  .
.
- [(C3)]
 contains at least two distinct points.
contains at least two distinct points.
Veblen and Whitehead showed that the axioms of group III imply the structure of a topological space in the sense of Hausdorff (including Hausdorff separability) [Veblen&Whitehead1931, p.95], [Veblen&Whitehead1932, p.79] and showed that their axioms were consistent and independent in the sense of Hilbert. Moreover, already in their article they announced that for class 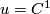 their axiom system allowed to serve as a logical basis for differential geometry, because in this class (or higher ones) ``it is possible to define a tangent space of differentials at each point of the manifold`` [Veblen&Whitehead1931, p.95].
their axiom system allowed to serve as a logical basis for differential geometry, because in this class (or higher ones) ``it is possible to define a tangent space of differentials at each point of the manifold`` [Veblen&Whitehead1931, p.95].
The last goal was achieved in their booklet on the Foundations of Differential Geometry published a year later (Veblen/Whitehead 1932). This book contributed effectively to a conceptual standardization of modern differential geometry and laid secure ground for the future development of differential topology. Not only did it contain the basic concepts of continuous and differentiable manifolds of different classes, but also the``modern`` reconstruction of the differentials 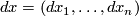 as objects in tangent spaces to
as objects in tangent spaces to  .[2] Basic concepts like Riemannian metric, affine connection, holonomy group, covering manifolds etc. followed in a formally satisfying symbolical precision. Even from the logical standards of the 1930s there remained no doubt that differential geometry in manifolds was logically well founded.
.[2] Basic concepts like Riemannian metric, affine connection, holonomy group, covering manifolds etc. followed in a formally satisfying symbolical precision. Even from the logical standards of the 1930s there remained no doubt that differential geometry in manifolds was logically well founded.
[edit] 3 Continuous and differentiable structures at the turn to the 1930s
Some years before Veblen's and Whitehead's axiomatization of the manifold concept the question of how to proceed from a given topological manifold to a differentiable one was a mystery. In an essay written in 1925 as a contribution for a planned Russian edition of collected works of N.I. Lobachevsky, H. Weyl described the status of the concept of continous manifold as ``somehow clarified (im mathematischer Hinsicht einigermaßen geklärt)``.[3] But he reminded the readers that for differential geometry, so important for the contemporary studies of general relativity, differentiability of coordinate transformations was presupposed. He emphasized that one ``must not take this requirement lightly``. As far as physical geometry was concerned, the recently achieved insight into the fundamental import of quantum physics led him to consider this requirement even as highly problematic. He warned:
It remains a problem how the real meaning of this state of affairs should be formulated with precision. It has to be conceded that, up to now, nearly nothing has been achieved with regard to the question of the meaning of differentiability in its applicability to reality. ([Weyl1925, 12, translation ES)]
By Veblen's and Whitehad's contribution differentiable manifolds became accessible to anybody acquainted with the language and symbolic practices of modern mathematics. Their characterization of the structure of ``class  `` left it open to expect that the transition from the continuous structure of a manifold to differentiable ones might be just a question of properly restricting the underlying pseudogroup. But the mathematicians of the late 19th century had learned to face the insight that for real functions the situation was quite complicated. Poincaré had deplored the result in his famous complaint of putting ``en défault les raisonnements de nos pères`` [Poincaré1889, p.131].[4] Should one now expect that further investigations of manifolds might lead to a similar complications on a new level? Or was the situation closer to the constellation hinted at in Hilbert's fifth Paris problem? In formulating his question Hilbert had at least cautiously implied that, for the case of groups, there might be closer relationship between the continuous and the differentiable than for real functions.[5]
`` left it open to expect that the transition from the continuous structure of a manifold to differentiable ones might be just a question of properly restricting the underlying pseudogroup. But the mathematicians of the late 19th century had learned to face the insight that for real functions the situation was quite complicated. Poincaré had deplored the result in his famous complaint of putting ``en défault les raisonnements de nos pères`` [Poincaré1889, p.131].[4] Should one now expect that further investigations of manifolds might lead to a similar complications on a new level? Or was the situation closer to the constellation hinted at in Hilbert's fifth Paris problem? In formulating his question Hilbert had at least cautiously implied that, for the case of groups, there might be closer relationship between the continuous and the differentiable than for real functions.[5]
For manifolds the question was wide open. At the time (the 1930s) it must have appeared completely unclear how this question might be attacked and what might be the result.
[edit] 1 Acknowledgments
This original version of this page was written by Erhard Scholz.
[edit] 2 Footnotes
- ↑ For a more complete later definition of pseudogroups see, e.g., [Kobayashi&Nomizu1963].
- ↑ The authors still used the pre-Bourbakian terminology of ``contravariant`` vector for the objects in the tangent space.
- ↑ The essay was published posthumously by K. Chandrasekharan [Weyl1925].
- ↑ Quoted from [Volkert1986, p.133].
- ↑ Hilbert had asked ``inhowfar Lie's concept of continuous transformation groups might be accessible to our investigation also without the assumption of the differentiability of the function`` [Hilbert1900].
[edit] 3 References
- [Brouwer1911] L. E. J. Brouwer, Beweis der Invarianz der Dimensionenzahl, Math. Ann. 70 (1911), no.2, 161–165. MR1511615 Zbl 42.0416.02
- [Brouwer1911a] L. E. J. Brouwer, Über Abbildung von Mannigfaltigkeiten, Math. Ann. 71 (1911), no.1, 97–115. MR1511644 Zbl 42.0417.01
- [Cartan1904] E. Cartan, Sur la structure des groupes infinis de transformation, Ann. Sci. École Norm. Sup. (3) 21 (1904), 153–206. MR1509054 (French) Zbl 35.0176.04
- [Dehn&Heegaard1907] M. Dehn and P. Heegaard, Analysis situs, Enzyklopädie der Mathematischen Wissenschaften III AB3: (1907) 153–200. Zbl 38.0510.14
- [Ferreiros1999] J. Ferreirós, Labyrinth of thought, Birkhäuser Verlag, 1999. ISBN 3-7643-5749-5
- [Hausdorff1914] F. Hausdorff, Grundzüge der Mengenlehre, Leipzig: Veit. 1914. In [Hausdorff2002]. MR0031025 (11,88d) Zbl 1010.01031
- [Hilbert1900] D. Hilbert, Mathematische Probleme. Vortrag, gehalten auf dem internationalen Mathematiker-Congress zu Paris 1900, (German) Gött. Nachr. (1900) 253–297. Zbl 31.0068.03
- [Kneser1926] H. Kneser Die Topologie der Mannigfaltigkeiten Jahresberichte DMV 34: (1926) 1–14.
- [Kobayashi&Nomizu1963] S. Kobayashi and K. Nomizu, Foundations of differential geometry. Vol I, Interscience Publishers, a division of John Wiley & Sons, New York-London, 1963. MR1393940 (97c:53001a) Zbl 0508.53002
- [Poincaré1889] H. Poincarè, La logique et l'intuition dan la science mathématique et dan l'enseignement, L'enseignement mathématique 1 (1889) 157–162. Zbl 30.0080.03
- [Poincaré2010] H. Poincaré, Papers on topology, American Mathematical Society, 2010. MR2723194 Zbl 05796329
- [Rodriguez2006] L. Rodriguez, Friedrich Riesz' Beiträge zur Herausbildung des modernen mathematischen Konzepts abstrakter Räume. Synthese intellektueller Kulturen in Ungarn, Frankreich und Deutschland, Dissertationsschrift Universität Mainz 2006.
- [Sarkaria1999] K. S. Sarkaria, The topological work of Henri Poincaré, History of topology, 123–167, North-Holland, Amsterdam, 1999. MR674912 (000m:57001) Zbl 0959.54002
- [Scholz1999] E. Scholz, The concept of manifold, 1850--1950, History of topology, North-Holland (1999), 25–64. MR1674908 (2000k:57001) Zbl 0956.57002
- [Tietze1908] H. Tietze, Über die topologischen Invarianten mehrdimensionaler Mannigfaltigkeiten, Monatsh. Math. Phys. 19 (1908), no.1, 1–118. MR1547755 Zbl 39.0720.05
- [Veblen&Whitehead1931] O. Veblen and J. Whitehead, A set of axioms for differential geometry, Proc. Natl. Acad. Sci. USA 17 (1931), 551-561. Zbl 0003.13002
- [Veblen&Whitehead1932] O. Veblen and J. Whitehead, The foundations of differential geometry, Cambridge Tracts in Math. a. Math. Phys. 29) London: Cambridge Univ. Press. IX, 97 S., 1932. Zbl 0005.21801
- [Vietoris1926] L. Vietoris, Über den höheren Zusammenhang von kompakten Räumen und eine Klasse von Abbildungen, welche ihn ungeändert läßt., Proceedings Amsterdam 29 (1926), 1008-1013. Zbl 52.0595.02
- [Vietoris1928] L. Vietoris, Über die Symmetrie in den Zusammenhangszahlen kombinatorischer Mannigfaltigkeiten, Monatsh. Math. Phys. 35 (1928), no.1, 165–174. MR154952 Zbl 54.0600.01
- [Volkert1986] K. T. Volkert, Die Krise der Anschauung, Vandenhoeck & Ruprecht, 1986. MR0874115 (88f:01033) Zbl 0613.01005
- [Weyl1924] H. Weyl, Análysis situs combinatorio, Revista Mat. Hispano-Americana 6, 1–9, 33–41 (1924). Zbl 50.0373.03
- [Weyl1925] H. Weyl, Riemanns geometrische Ideen, ihre Auswirkung und ihre Verknüpfung mit der Gruppentheorie, Eidgenössische Technische Hochschule Zürich (Switzerland). Berlin etc.: Springer-Verlag 1988. Zbl 0649.53002
- [van Kampen1929] E. R. van Kampen, Die kombinatorische Topologie und die Dualitätssätze, Den Haag, Stockum & Zoon 1929. Zbl 55.0964.01
- [van der Waerden1930] B. L. van der Waerden, Kombinatorische Topologie., Jahresbericht DMV 39 (1930), 121-139. Zbl 56.0497.01